Home
Class 9
MATHS
P, Q, R and S are respectively the midpo...

P, Q, R and S are respectively the midpoints of the sides AB, BC, CD and DA of a quadrilateral ABCD. Show that
(i) PQ||AC and ` PQ=(1)/(2) AC `
(ii) PQ||SR
(iii) PQRS is a parallelogram .

Text Solution

Verified by Experts

In `triangle ABC`, P and Q are the midpoints of AB and BC respectively.
`therefore "PQ||AC and "PQ =(1)/(2) AC`. Similarly, SR||AC.
Promotional Banner

Topper's Solved these Questions

  • QUADRILATERALS

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|47 Videos

  • QUADRILATERALS

    RS AGGARWAL|Exercise MULTIPLE-CHOICE QUESTIONS (MCQ)|9 Videos

  • QUADRILATERALS

    RS AGGARWAL|Exercise EXERCISE 10B|27 Videos

  • PROBABILITY

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|16 Videos

  • TRIANGLES

    RS AGGARWAL|Exercise MULTIPLE-CHOICE QUESTIONS (MCQ)|10 Videos

Similar Questions

Explore conceptually related problems

P, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.

P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and ACbotBD . Prove that PQRS is a square.

ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : (i) S R\ ||\ A C and S R=1/2A C (ii) P Q\ =\ S R (iii) PQRS is a parallelogram.

Let P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD Show that PQRS is a parallelogram such that ar("||gm PQRS")=(1)/(2)ar("quad. ABCD") .

P, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that ar("|| gm PQRS")=(1)/(2)xxar("||gm ABCD) .

In a quadrilateral ABCD, show that (AB+BC+CD+DA)gt(AC+BD) .

P and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

ABCD is a rhombus and P, Q, R and S are ©wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

In a quadrilateral ABCD, show that (AB+BC+CD+DA)lt2(BD+AC).

The midpoints of the sides AB,BC,CD and DA of a quadrilateral ABCD are joined to form a quadrilateral.If AC=BD and AC perp BD then prove that the quadrilateral formed is a square.

RS AGGARWAL-QUADRILATERALS-EXERCISE 10C
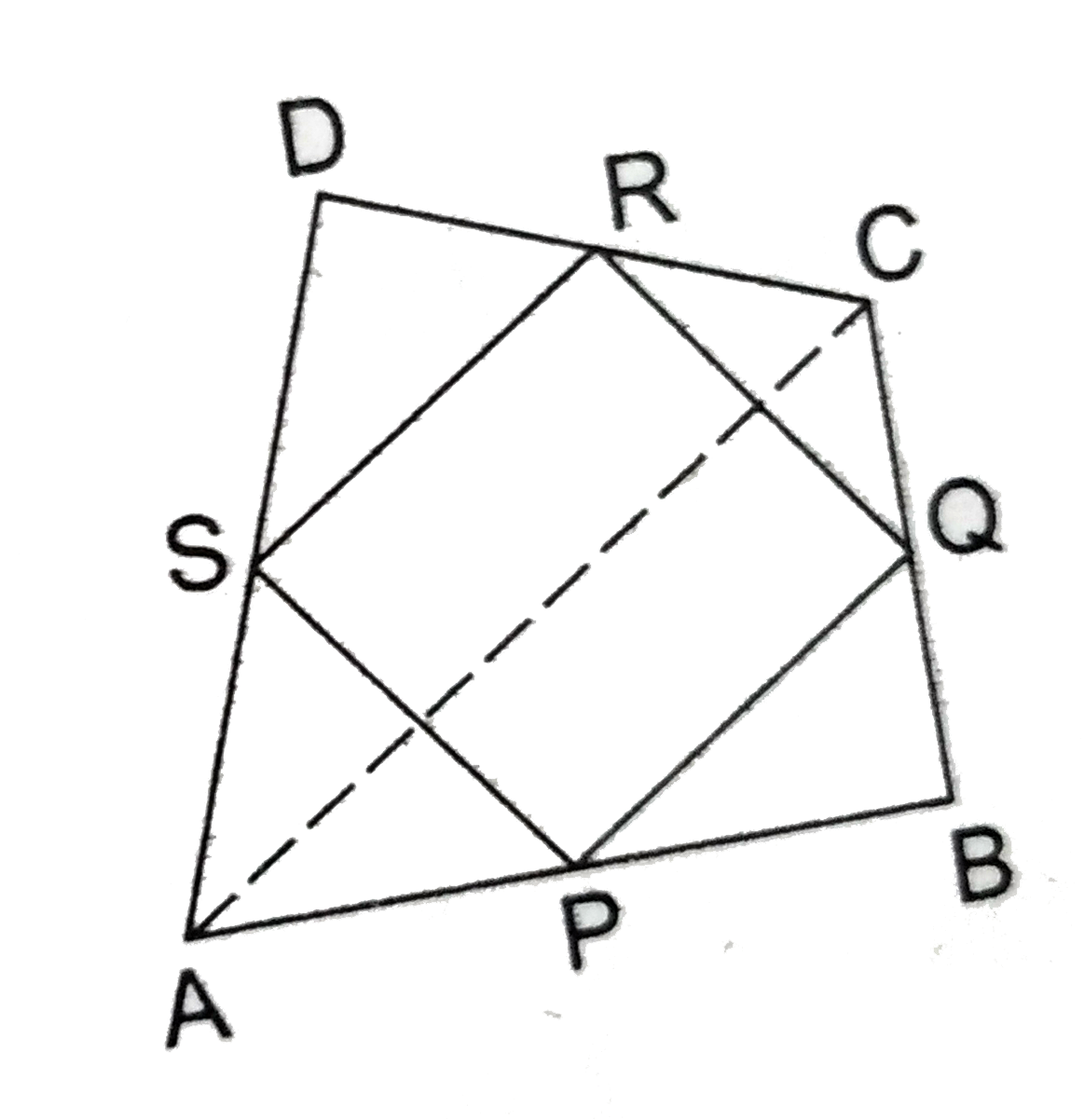
  1. P, Q, R and S are respectively the midpoints of the sides AB, BC, CD a...

    Text Solution

    |

  2. A square is inscribed in an isosceles right triangle so that the squar...

    Text Solution

    |

  3. ABCD is a parallelogram, E and F are the mid-points of AB and CD respe...

    Text Solution

    |

  4. M and N are points on opposite sides AD and BC of a parallelogram ABCD...

    Text Solution

    |

  5. In the adjoining figure, PQRS is a trapezium in which PQ||SR and M is ...

    Text Solution

    |

  6. In a parallelogram PQRS, PQ = 12 cm and PS = 9 cm. The bisector of ang...

    Text Solution

    |

  7. In the adjoining figure, ABCD is a trapezium in which AB||DC and P,...

    Text Solution

    |

  8. In the adjoining figure, AD is a median of triangle ABC and DE||BA. Sh...

    Text Solution

    |

  9. In the adjoining figure, AD and BE are the medians of triangle ABC an...

    Text Solution

    |

  10. Show that the diagonals of a parallelogram divide it into four tria...

    Text Solution

    |

  11. In the adjoining figure, D, E, F are the midpoints of the sides BC, CA...

    Text Solution

    |

  12. Show that the quadrilateral formed by joining the mid-points of the ...

    Text Solution

    |

  13. prove using vectors: The quadrilateral obtained by joining mid-poin...

    Text Solution

    |

  14. Show that the quadrilateral, formed by joining the mid-points of the ...

    Text Solution

    |

  15. Show that the line segments joining the mid-points of the opposite ...

    Text Solution

    |

  16. The diagonals of a quadrilateral ABCD are equal. Prove that the quard...

    Text Solution

    |

  17. The diagonals of a quadrilateral A B C D are perpendicular. Show that ...

    Text Solution

    |

  18. The midpoints of the sides AB, BC, CD and DA of a quadrilateral ABCD a...

    Text Solution

    |