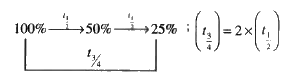A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
NUCLEAR CHEMISTRY
AAKASH SERIES|Exercise LECTURE SHEET (LEVEL- II) (EXERCISE - III) (Match the following questions )|3 VideosNUCLEAR CHEMISTRY
AAKASH SERIES|Exercise LECTURE SHEET (LEVEL- II) (EXERCISE - IV) (Integer answer type Questions)|9 VideosNUCLEAR CHEMISTRY
AAKASH SERIES|Exercise PRACTICE SHEET - 2 (Integer answer type Questions )|8 VideosNOBLE GASES
AAKASH SERIES|Exercise PRACTICE SHEET - 2 (Single more than one option questions)|5 VideosPERIODIC TABLE
AAKASH SERIES|Exercise QUESTIONS FOR DESCRIPTIVE ANSWERS|37 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-NUCLEAR CHEMISTRY -LECTURE SHEET (LEVEL- II) (EXERCISE - II) (Linked Comprehension type questions)
- Radioactive decay is a statisticle process i.e., we cannot precisely p...
Text Solution
|
- Radioactive decay is a statisticle process i.e., we cannot precisely p...
Text Solution
|
- Radioactive decay is a statisticle process i.e., we cannot precisely p...
Text Solution
|
- The emission of penetraing alpha , betaparticle (""(2) ^(4) He and ""...
Text Solution
|
- The emission of penetraing alpha , betaparticle (""(2) ^(4) He and ""...
Text Solution
|
- The emission of penetraing alpha , betaparticle (""(2) ^(4) He and ""...
Text Solution
|
- It has been estimated that the total power radiated by the sun is 3.8 ...
Text Solution
|
- It has been estimated that the total power radiated by the sun is 3.8 ...
Text Solution
|
- It has been estimated that the total power radiated by the sun is 3.8 ...
Text Solution
|