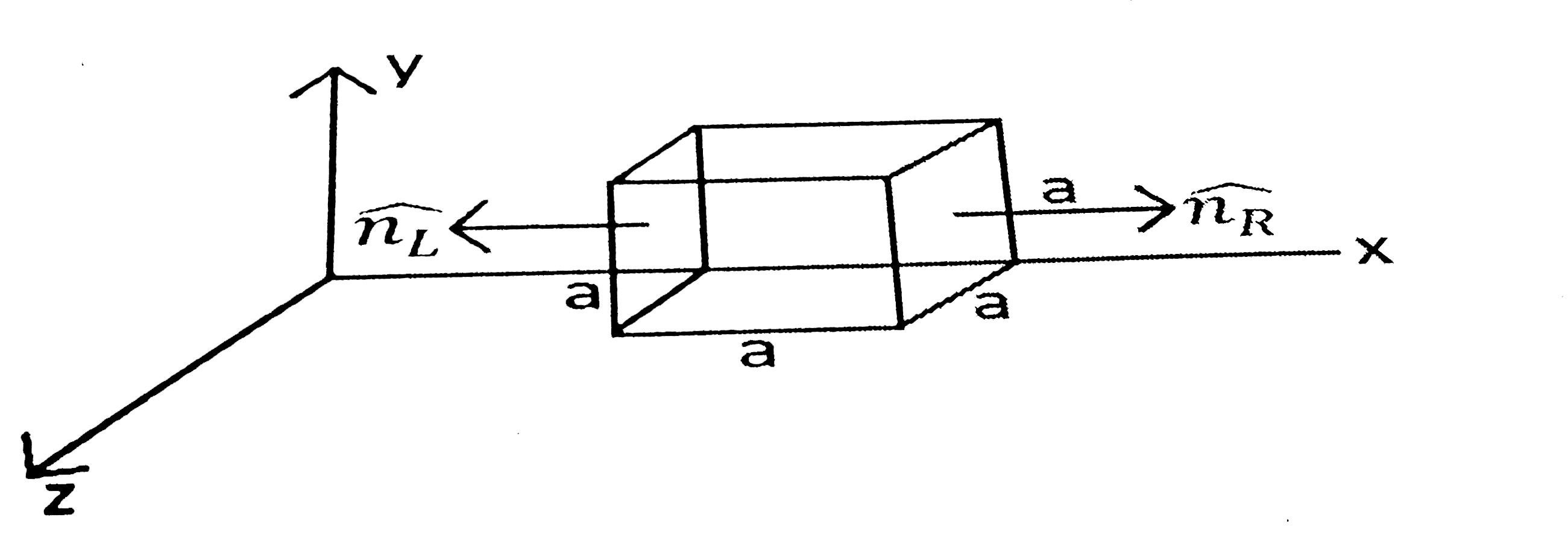
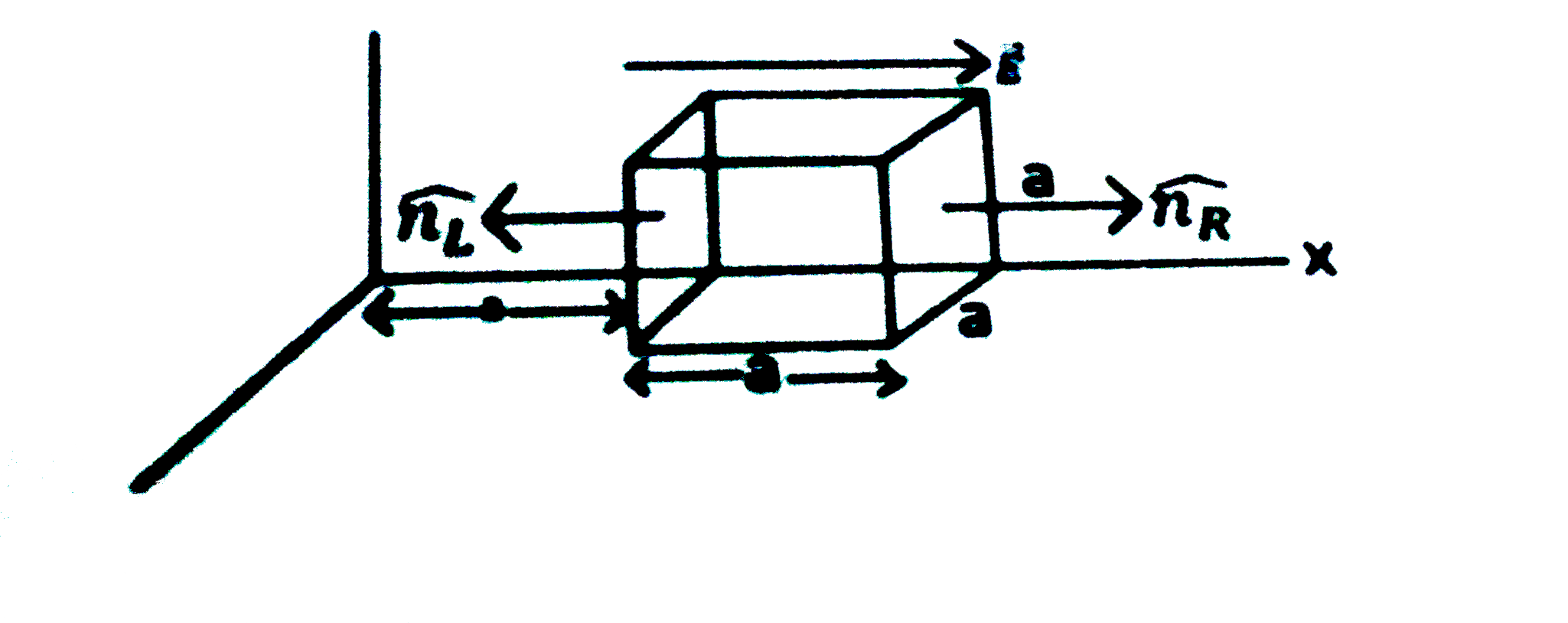
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
XII BOARD PREVIOUS YEAR PAPER ENGLISH-SAMPLE PAPER 2019-SECTION D
- Using Gauss’s law, derive expression for intensity of electric field a...
Text Solution
|
- Define electrostatic potential at a point. Write its SI unit Three ...
Text Solution
|
- The arm PQ of the rectangular conductor is moved from x=0, outwards in...
Text Solution
|
- Write working principle of cyclotron and with a suitable diagram expla...
Text Solution
|
- Derive mirror equation for a convex mirror. Using it, show that a conv...
Text Solution
|
- (a) Draw a ray diagram for final image formed at distance of distinct ...
Text Solution
|