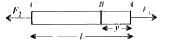A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
LAWS OF MOTION
MTG GUIDE|Exercise NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (LAW OF CONSERVATION OF LINEAR MOMENTUM AND ITS APPLICATIONS)|6 VideosView PlaylistLAWS OF MOTION
MTG GUIDE|Exercise NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (EQUILIBRIUM OF CONCURRENT FORCES)|7 VideosView PlaylistLAWS OF MOTION
MTG GUIDE|Exercise AIPMT /NEET (MCQ)|24 VideosView PlaylistKINEMATICS
MTG GUIDE|Exercise AIPMT/ NEET MCQs|31 VideosView PlaylistMOTION OF SYSTEM OF PARTICLES AND RIGID BODY
MTG GUIDE|Exercise AIPMT / NEET (MCQs)|37 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
MTG GUIDE-LAWS OF MOTION-NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) ( NEWTON.S LAWS OF MOTION)
- A cricketer catches a ball of mass 150 gm. in 0.1 second moving with s...
02:16
|
Play - Two masses M(1)=5kg,M(2)=10kg are connected at the ends of an inextens...
02:08
|
Play - A rod of length L and mass M is acted on by two unequal forces F1 and ...
Text Solution
|
Playing Now - A book is lying on the table. What is the angle belween the action of ...
02:15
|
Play - When a force F acs on a body of mass m the acceleration product in the...
02:37
|
Play - The ratio of the weight of a man in a stationary lift and when it is m...
02:11
|
Play - A block released from rest from the top of a smooth inclined plane of ...
07:20
|
Play - A block of weight 4 kg is resting on a smooth horizontal plane. If it ...
03:20
|
Play - A body of mass 5 kg is acted on by a net force F which varies with tim...
02:26
|
Play - A dynamometer D, which is a device used to measure force, is attached ...
02:47
|
Play - A string of length L and mass M is lying on a horizontal table. A forc...
03:21
|
Play - Three equal weight A,B and C of mass 2kg each are hanging on a string ...
02:11
|
Play - Two blocks of masses of 40 kg and 30 kg are connected by a weightless ...
04:32
|
Play - Sand particles drop vertically at the rate of 2kgs^-1 on a conveyor be...
01:29
|
Play - In the system shown in the figure, the acceleration of 1 kg block is
05:16
|
Play - An object is kept on a smooth inclined plane of height 1 unit and len...
08:24
|
Play - A body, under the action of a force vec(F)=6hati -8hatj+10hatk , acqui...
01:47
|
Play - Figure shows a man standing stationary with respect to a horizontal co...
01:30
|
Play - In the arrangement shown in the Fig, the ends P and Q of an unstretcha...
06:41
|
Play - A player caught a cricket ball of mass 150g moving at a rate of 20m//s...
02:17
|
Play