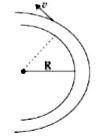
A
B
C
D
Text Solution
Verified by Experts
|
Topper's Solved these Questions
JEE MAIN 2021
JEE MAINS PREVIOUS YEAR|Exercise PHYSICS (SECTION B)|30 VideosView PlaylistJEE MAIN 2021
JEE MAINS PREVIOUS YEAR|Exercise PHYSICS SECTION A|60 VideosView PlaylistJEE MAIN 2021
JEE MAINS PREVIOUS YEAR|Exercise (SECTION - B)|10 VideosView PlaylistJEE MAIN
JEE MAINS PREVIOUS YEAR|Exercise All Questions|473 VideosView PlaylistJEE MAIN 2022
JEE MAINS PREVIOUS YEAR|Exercise Question|492 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
JEE MAINS PREVIOUS YEAR-JEE MAIN 2021-PHYSICS (SECTION A)
- An AC current is given by I = I(1) sin omega t + I(2) cos omega t A h...
03:09
|
Play - Two ideal polyatomic gases at temperature T(1) and T(2) are mixed so t...
03:15
|
Play - A modern gran -prix racing car of masses m is travelling on a flat tra...
05:51
|
Playing Now - The output of the given combination gates represents :
03:32
|
Play - The diameter of a plano convex lens is 6 cm and thickness at the centr...
03:33
|
Play - An electron of mass m and a photon have same energy E. The ratio of w...
02:56
|
Play - A current of 10 A exists in a wire of crossectional area of 5 m m^(2) ...
02:26
|
Play - When two soap bubbles of radii a and b ( b gt a ) coalesce, the radius...
02:35
|
Play - A solenoid of 1000 turns per metre has a core with relative permeabil...
02:55
|
Play - A triangular plate is shown. A force vec( F ) = 4 hat(i) - 3 hat(j) is...
03:43
|
Play - Which level of the single ionized carbon has the same energy as the gr...
01:39
|
Play - A boy is rolling a 0.5 kg ball on the frictionless floor with the spee...
02:23
|
Play - In a seris LCR circuit, the inductive reactance (X(L)) is 10 Omega and...
02:48
|
Play - For an adiabatic expansion of an ideal gas, the fractional change in i...
02:39
|
Play - If the angular velocity of earth's spin is increased such that the bod...
05:33
|
Play - An object of mass m(1) collides with another object of mass m2, which ...
05:21
|
Play - A plane electromagnetic wave propagating along y-direction can have th...
02:02
|
Play - Which of the following statements are correct? (A) Electric monopole...
06:53
|
Play - A solid cylinder of mass m is wrapped with an inextensible light strin...
04:10
|
Play - The correct relation between alpha (ratio of collector current to emit...
02:25
|
Play