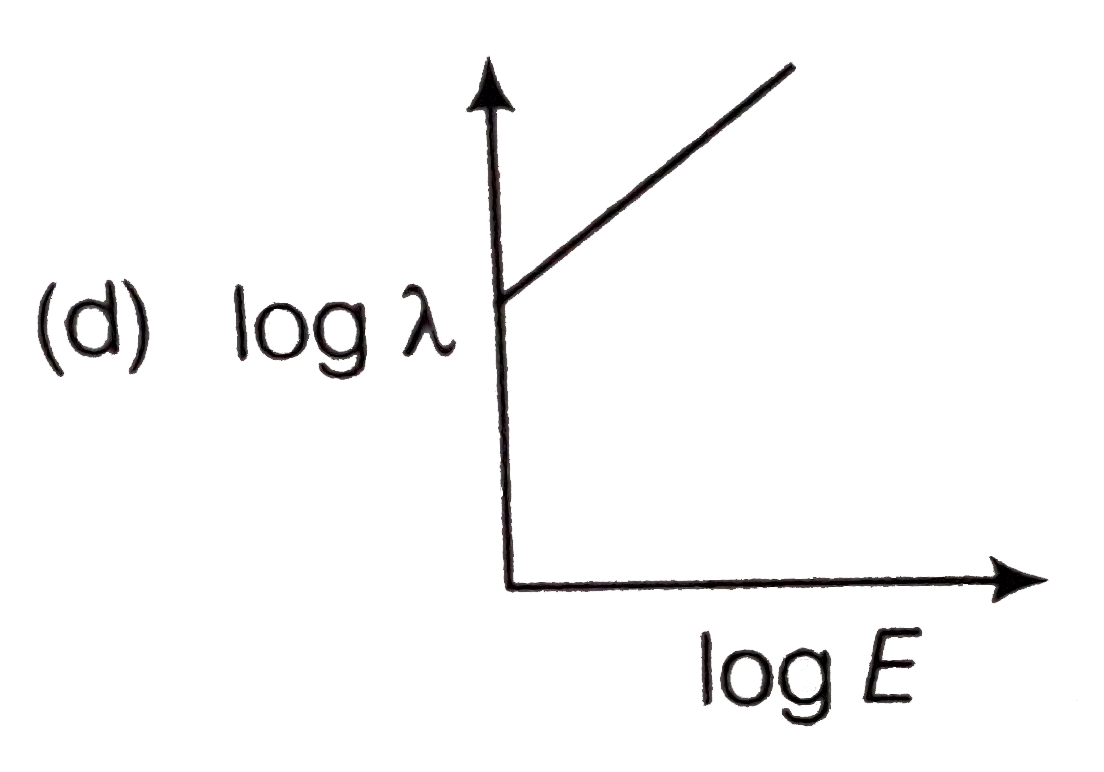A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
SOLVED PAPERS 2018
DC PANDEY ENGLISH|Exercise Assertion and Reasons|10 VideosView PlaylistSOLVED PAPERS 2018
DC PANDEY ENGLISH|Exercise JIPMER|22 VideosView PlaylistSOLVED PAPERS 2018
DC PANDEY ENGLISH|Exercise JIPMER|22 VideosView PlaylistSOLVED PAPER 2017
DC PANDEY ENGLISH|Exercise Solved papers 2017(JIPMER)|32 VideosView PlaylistWAVE OPTICS
DC PANDEY ENGLISH|Exercise For JEE Advanced E. Integer Type Questions|13 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-SOLVED PAPERS 2018-AIIMS
- Positive charge Q is distributed uniformly over a circular ring of rad...
03:32
|
Play - An infinite number of identical capacitors each of capacitance 1 mF ar...
04:07
|
Play - In the circuit in fig. If no current flows through the galvanometer wh...
03:12
|
Play - In a series C-R circuit shown in figureure, the applied voltage is 10 ...
02:32
|
Play - A system S consists of two coils A and B. The coil, A carries a steady...
01:29
|
Play - A long straight wire, carrying current I, is bent at its midpoint to f...
06:39
|
Play - An element dvecl=dxhati (where dx=1cm) is placed at the origin and car...
03:44
|
Play - The coil in figure carries current i=2.00 A in the direction indicated...
05:10
|
Play - Consider the following figure, a uniform magnetic field of 0.2 T is di...
02:18
|
Play - An idal coil of 10 is connected in series with a resitance of 5Omega a...
02:01
|
Play - In the circuit, shown the galvanometer G of resistance 60Omega is shif...
02:11
|
Play - In a circuit L, C and R are connected in series with an alternating vo...
02:01
|
Play - The log - log graph between the energy E of an electron and its de - B...
02:57
|
Playing Now - The half life of a radioactive substance is 20 minutes . The approxima...
02:36
|
Play - The diode used at a constant potential drop of 0.5 V at all currents a...
02:40
|
Play - An upolarised beam of intensity 2a^(2) passes through a thin polarioid...
01:57
|
Play - A hydrogen like atom of atomic number Z is in and excited state of qua...
07:01
|
Play - A diode detector is used to detect an amplitude modulated wave of 60% ...
01:20
|
Play - A circular loop of radius 0.3 cm lies parallel to amuch bigger circula...
04:01
|
Play - In the adjoining circuit diagram, the readings of ammeter and voltmete...
02:42
|
Play