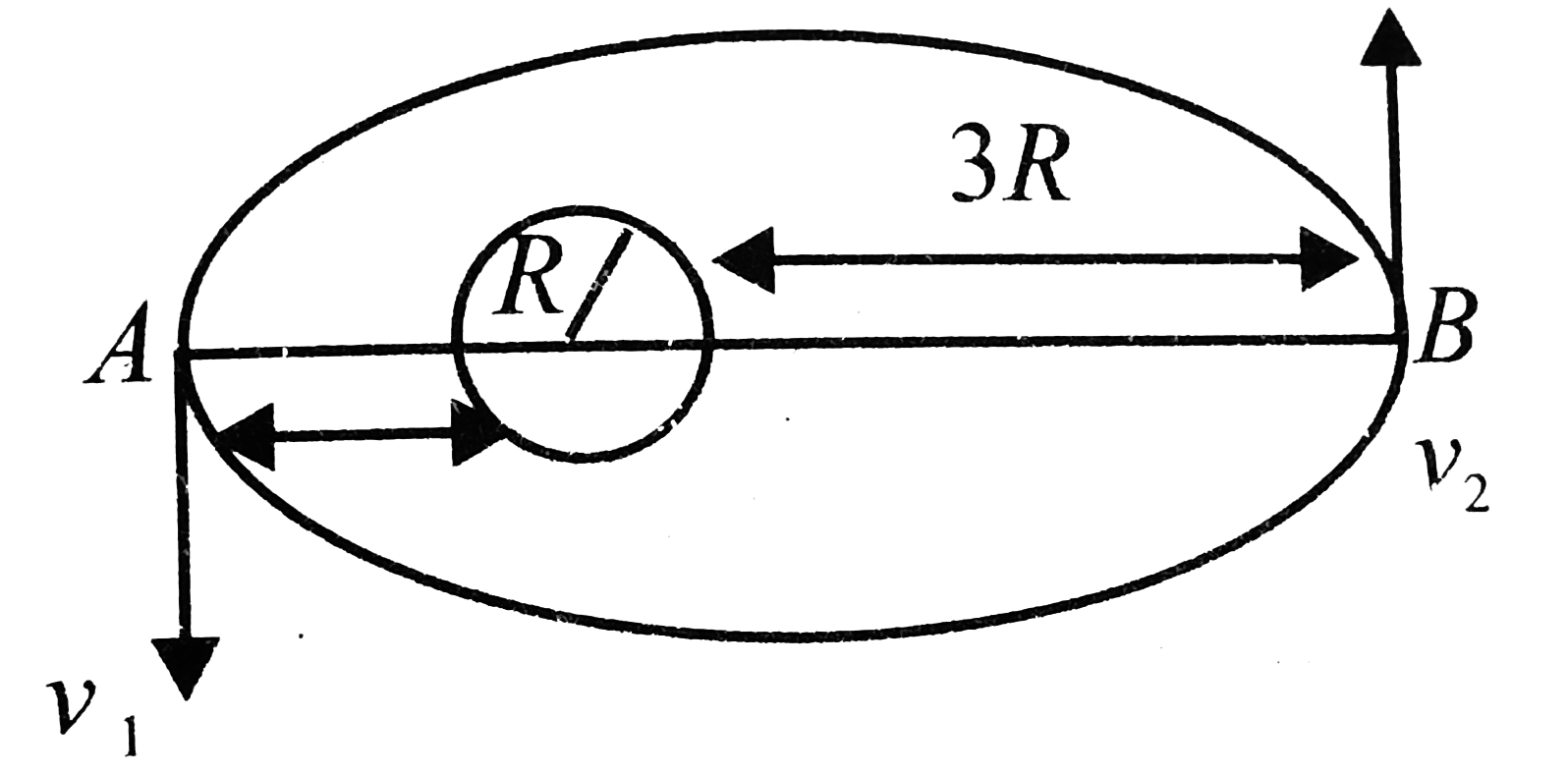
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise Integer|5 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise Fill In The Blanks|5 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise Assertion- Reasoning|13 VideosFLUID MECHANICS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-GRAVITATION-Linked Comprehension
- The minimum and maximum distances of a satellite from the center of th...
Text Solution
|
- The orbit of Pluto is much more eccentric than the orbits of the other...
Text Solution
|
- The orbit of Pluto is much more eccentric than the orbits of the other...
Text Solution
|
- The orbit of Pluto is much more eccentric than the orbits of the other...
Text Solution
|
- A solid sphere of mass m and radius r is placed inside a hollow thin s...
Text Solution
|
- a solid sphere of mass m and radius r is placed inside a hollow thin s...
Text Solution
|
- A solid sphere of mass m and radius r is placed inside a hollow thin s...
Text Solution
|
- The gravitational field in a region is given by vecE=(5Nkg^-1)veci+(12...
Text Solution
|
- The gravitational field in a region is given by vecE=(5Nkg^-1)veci+(12...
Text Solution
|
- The gravitational field in a region is given by vecE=(5Nkg^-1)veci+(12...
Text Solution
|
- The gravitational field in a region is given by vecE=(5Nkg^-1)veci+(12...
Text Solution
|
- A uniform metal sphere of radius R and mass m is surrounded by a thin ...
Text Solution
|
- A uniform metal sphere of radius R and mass m is surrounded by a thin ...
Text Solution
|
- In the graph shown, the PE of earth-satellite system is shown by a sol...
Text Solution
|
- In the graph shown, the PE of earth-satellite system is shown by a sol...
Text Solution
|
- In the graph shown, the PE of earth-satellite system is shown by a sol...
Text Solution
|
- An unmanned satellite A and a spacecraft B are orbiting around the ear...
Text Solution
|
- An unmanned satellite A and a spacecraft B are orbiting around the ear...
Text Solution
|
- An unmanned satellite A and a spacecraft B are orbiting around the ear...
Text Solution
|
- An unmanned satellite A and a spacecraft B are orbiting around the ear...
Text Solution
|