Home
Class 12
PHYSICS
A cylindrical cavity of diameter a exist...

A cylindrical cavity of diameter a exists inside a cylinder of diameter `2a` as shown in the figure. Both the cylinder and the cavity are infinitity long. A uniform current density `j` flows along the length . If the magnitude of the magnetic field at the point `P` is given by `(N)/(12) mu_(0)Ja`, then the value of `N` is

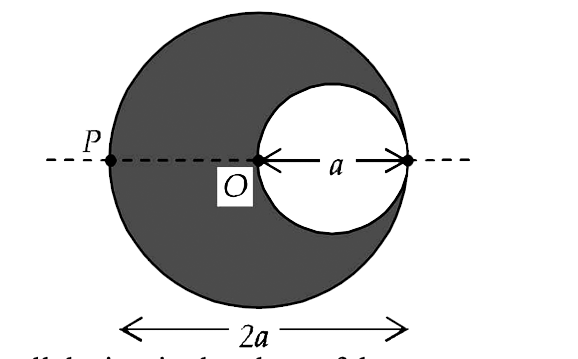
Text Solution

Verified by Experts

The correct Answer is:
`(5)`
(5) `B_1=(mu_Jpia^2)/(2pia)=(mu_0Ja)/2,B_2=(mu_Jpi(a//2)^2)/(2pi(3a//2))=(mu_0Ja)/12`
`B_1-B_2=(mu_Ja)/2-(mu_Ja)/12`
`=((mu_0Ja)/2)(1-1/6)=5/6((mu_0Ja)/2)=(5mu_0aJ)/12`
`=N/12mu_0aJ`
`:. N=5`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • SOURCES OF MAGNETIC FIELD

    CENGAGE PHYSICS ENGLISH|Exercise Subjective type|10 Videos

  • SOURCES OF MAGNETIC FIELD

    CENGAGE PHYSICS ENGLISH|Exercise single correct Answer Type|35 Videos

  • SOURCES OF MAGNETIC FIELD

    CENGAGE PHYSICS ENGLISH|Exercise Archives (linked Comprehension)|4 Videos

  • RAY OPTICS

    CENGAGE PHYSICS ENGLISH|Exercise DPP 1.6|12 Videos

  • WAVE OPTICS

    CENGAGE PHYSICS ENGLISH|Exercise Comprehension Type|14 Videos

Similar Questions

Explore conceptually related problems

A cylinderical cavity of diameter a exists inside a cylinder of diameter 2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given by (N)/(12)mu_(0)aJ , then the value of N is

An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius (R)/(2) are shown in the figure. The remaining portion has uniform volume charge density rho . The magnitude of electrical field at the centre of the cavity is-

Knowledge Check

  • Inside a long straight uniform wire of round cross-section, there is a long round cylindrical cavity whose axis is parallel to the axis of the wire and displaced from the latter by a distance l. A direct current of density j flows along the wire. Find the magnetic induction inside the cavity. Consider, in particular, the case l=0 .

    A
    0
    B
    `1/2mu_(0) vecJ xx vecd`
    C
    `mu_(0) vecJ xx vecd`
    D
    `3/2mu_(0) vecJ xx vecd`

    • Similar Questions

    Explore conceptually related problems

    A thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.

    An infinitely long hollow conducting cylinder with inner radius (R)/(2) and outer radius R carries a uniform current density along its length . The magnitude of the magnetic field , | vec(B)| as a function of the radial distance r from the axis is best represented by

    Two co-axial hollow cylinders of radius a and 2a having current I and 3I/2 in opposite directions respectively as shown in the figure. The ratio of the magnitude of magnetic field at the point P and point Q will be (OP= 3a/2 and OQ=5a/2)

    A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J = kr^(2) , where, k is a constant. Find an expression for the magnetic field B at a distance r (lt R) from the axis

    A thin sheet of width 2a is placed in the x-y plane between the lines x=-a and x=a . The sheet is very long in the -y and +y directions. It carries a current l towards the +y direction. This current is uniformly distributed over the width of the sheet. The magnitude of magnetic fiedl at the point P(2a,0) due to the sheet is (1/n)((mu_(0)I)/(pia))log_(e)3 . Here the value of n is ______________.

    Four very long wires are arranged as shown in the figure, so that their cross - section forms a square, with connections at the ends so that current I flow through all four wires. Length of each side of the formed such square is b. The magnetic field at the central point P (centre of the square) is

    An infinitely long solid cylinder of radius R has a uniform volume charge density rho . It has a spherical cavity of radius R//2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P , which is at a distance 2 R form the axis of the cylinder, is given by the expression ( 23 r R)/( 16 k e_0) . The value of k is . .

    Home
    Profile