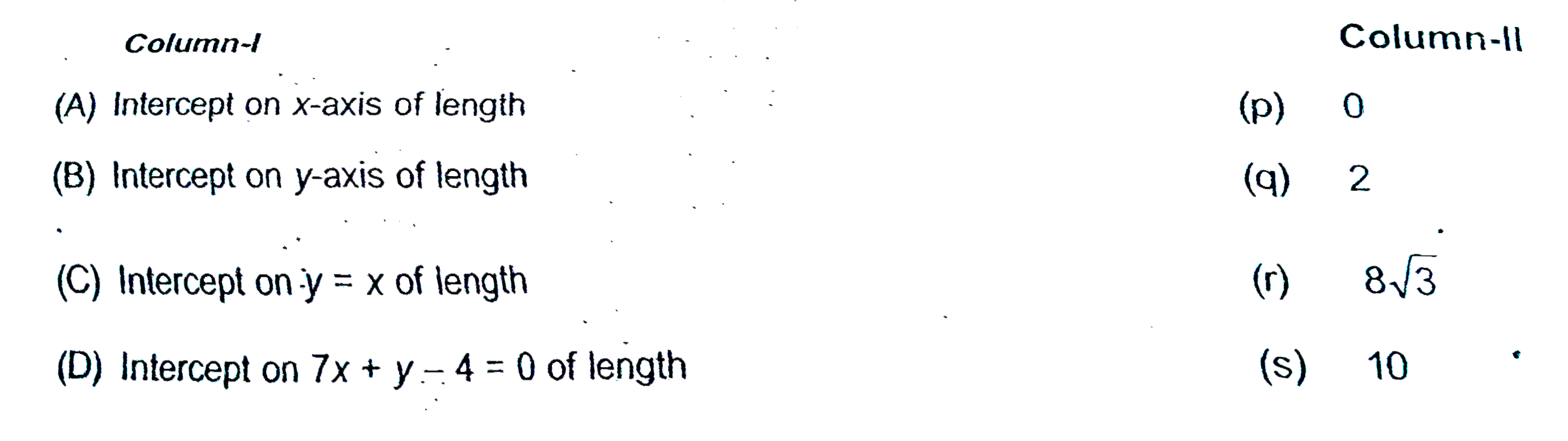Home
Class 12
MATHS
x^(2) + y^(2) - 14x - 10y + 24 = 0 makes...

`x^(2) + y^(2) - 14x - 10y + 24 = 0` makes an

Text Solution

Verified by Experts

The correct Answer is:
A(s), B(q), C(r ), D(p)
Promotional Banner

Topper's Solved these Questions

  • CONIC SECTIONS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION-G ( Integer Answer Type Questions )|12 Videos

  • CONIC SECTIONS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION - H ( Multiple True-False Type Questions )|5 Videos

  • CONIC SECTIONS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION -E ( Assertion-Reason Type Questions )|18 Videos

  • COMPLEX NUMBERS AND QUADRATIC EQUATIONS

    AAKASH INSTITUTE ENGLISH|Exercise section-J (Aakash Challengers Qestions)|13 Videos

  • CONTINUITY AND DIFFERENTIABILITY

    AAKASH INSTITUTE ENGLISH|Exercise section - J|6 Videos

Similar Questions

Explore conceptually related problems

Find the transverse common tangents of the circles x^(2) + y^(2) -4x -10y + 28 = 0 and x^(2) + y^(2) + 4x - 6y + 4= 0.

If the two circles x^(2) + y^(2) =4 and x^(2) +y^(2) - 24x - 10y +a^(2) =0, a in I , have exactly two common tangents then the number of possible integral values of a is : A. 0 B. 2 C. 11 D. 13

Prove that the circles x^(2) +y^(2) - 4x + 6y + 8 = 0 and x^(2) + y^(2) - 10x - 6y + 14 = 0 touch at the point (3,-1)

The equation (s) of common tangents (s) to the two circles x^(2) + y^(2) + 4x - 2y + 4 = 0 and x^(2) + y^(2) + 8x - 6y + 24 = 0 is/are

The least distance between two points P and Q on the circle x^(2) + y^(2) -8x + 10y + 37 =0 and x^(2) + y^(2) + 16x + 55 = 0 is _______ .

The number of common tangents to the circles x^2 + y^2 - 4x + 6y + 8 = 0 and x^2 + y^2 - 10x - 6y + 14 = 0 is : (A) 2 (B) 3 (C) 4 (D) none of these

Find the angle between the circles x^2 + y^2 + 4x - 14y + 28 = 0 and x^2 + y^2 + 4x - 5 = 0

The locus of the centre of the circle cutting the circles x^2+y^2–2x-6y+1=0, x^2 + y^2 - 4x - 10y + 5 = 0 orthogonally is

The circle with centre (1, 2) cuts the circle x^2 + y^2 + 14x - 16y + 77 = 0 orthogonally then its radius is

Find the centre and the radius of the circles 3x^(2) + 3y^(2) - 8x - 10y + 3 = 0