Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) FILL IN THE BLANKS TYPE|6 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) TRUE/FALSE|1 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive)MATCH MATRIX|1 VideosGASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise JEE ADVANCED (ARCHIVE )|111 VideosINTRODUCTION TO VECTORS & FORCES
VMC MODULES ENGLISH|Exercise JEE Advanced ( ARCHIVE LEVEL-2)|12 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-GRAVITATION-JEE Advance (Archive) NUMERICAL ANSWER
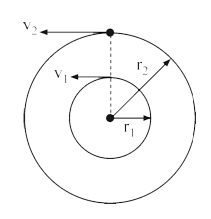
- Two satellite S1 and S2 revolve round a planet in coplanar circular or...
Text Solution
|
- Three particles each of mass m, are located at the vertices of an equi...
Text Solution
|
- An artificial satellite is moving in a circular orbit around the earth...
Text Solution
|
- Mass M, of a planet earth is uniformly distributed over a spherical vo...
Text Solution
|
- Distance between the centres of two stars is 10a. The masses of these ...
Text Solution
|
- A body is projected vartically upwards from the bottom of a crater of ...
Text Solution
|
- A binary star consists of two stars A(mass 2.2 Ms) and B (mass 11 Ms)...
Text Solution
|
- Gravitational acceleration on the surface of a planet is (sqrt6)/(11)g...
Text Solution
|
- A bullet is fired vertically upwards with velocity v from the surface ...
Text Solution
|
- A large spherical mass M is fixed at one position and two identical po...
Text Solution
|