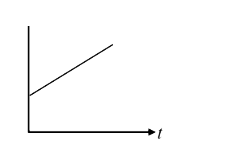
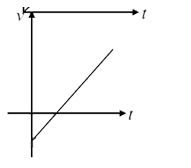
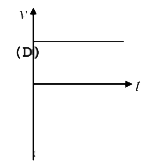
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
KINEMATICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise LEVEL 2|65 VideosView PlaylistKINEMATICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise JEE MAIN (archive)|19 VideosView PlaylistKINEMATICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise JEE Advanced (archive)|14 VideosView PlaylistJEE MAIN REVISON TEST-23
VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|1 VideosView PlaylistLAWS OF MOTION
VMC MODULES ENGLISH|Exercise IMPECCABLE|53 VideosView Playlist
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-KINEMATICS OF A PARTICLE -LEVEL 1
- A body starts from the origin and moves along the X-axis such that the...
05:31
|
Play - A particle is projected with velocity v(0) along x - axis. The deceler...
03:03
|
Play - Which of the following represents uniformly accelerated motion ?
00:44
|
Play - The position-time relation of a particle moving along the x-axis is gi...
01:47
|
Playing Now - If the velocity v of a particle moving along a straight line decreases...
03:44
|
Play - For a body thrown vertically upwards, if the air resistance is taken i...
02:53
|
Play - A particle is thrown upwards from ground. It experiences a constant re...
03:18
|
Play - Assertion: Two bodies of masses M and m(M gt m) are allowed to fall fr...
03:31
|
Play - A bus moves over a straight level road with a constant acceleration a....
03:30
|
Play - A ball A is thrown vertically upwards with speed u. At the same instan...
01:39
|
Play - A body X is projected upwards with a velocity of 98 ms^(-1), after 4s,...
06:51
|
Play - Two cars A and B are at rest at same point initially. If A starts with...
01:58
|
Play - A man is 45m behind the bus when the bus start accelerating from rest ...
01:45
|
Play - Two cars A and B are travelling in the same direction with velocity up...
01:13
|
Play - Two objects are moving along the same straight line. They cross a poin...
02:15
|
Play - P, Q and R are three balloons ascending with velocities U, 4U and 8U r...
06:17
|
Play - Two identical balls are shot upward one after another at an interval o...
02:11
|
Play - Two balls are dropped from different heights at different instants. Se...
02:23
|
Play - Two bodies begin to fall freely from the same height but the second fa...
02:33
|
Play - A bird files between two trains approaching each other with constant s...
03:03
|
Play