Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)|14 VideosROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (True/False Type)|3 VideosROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (MATRIX MATCH TYPE)|1 VideosREVISION TEST-2 JEE
VMC MODULES ENGLISH|Exercise PHYSICS|25 VideosSIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise 7-previous year question|46 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-ROTATIONAL MOTION -JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
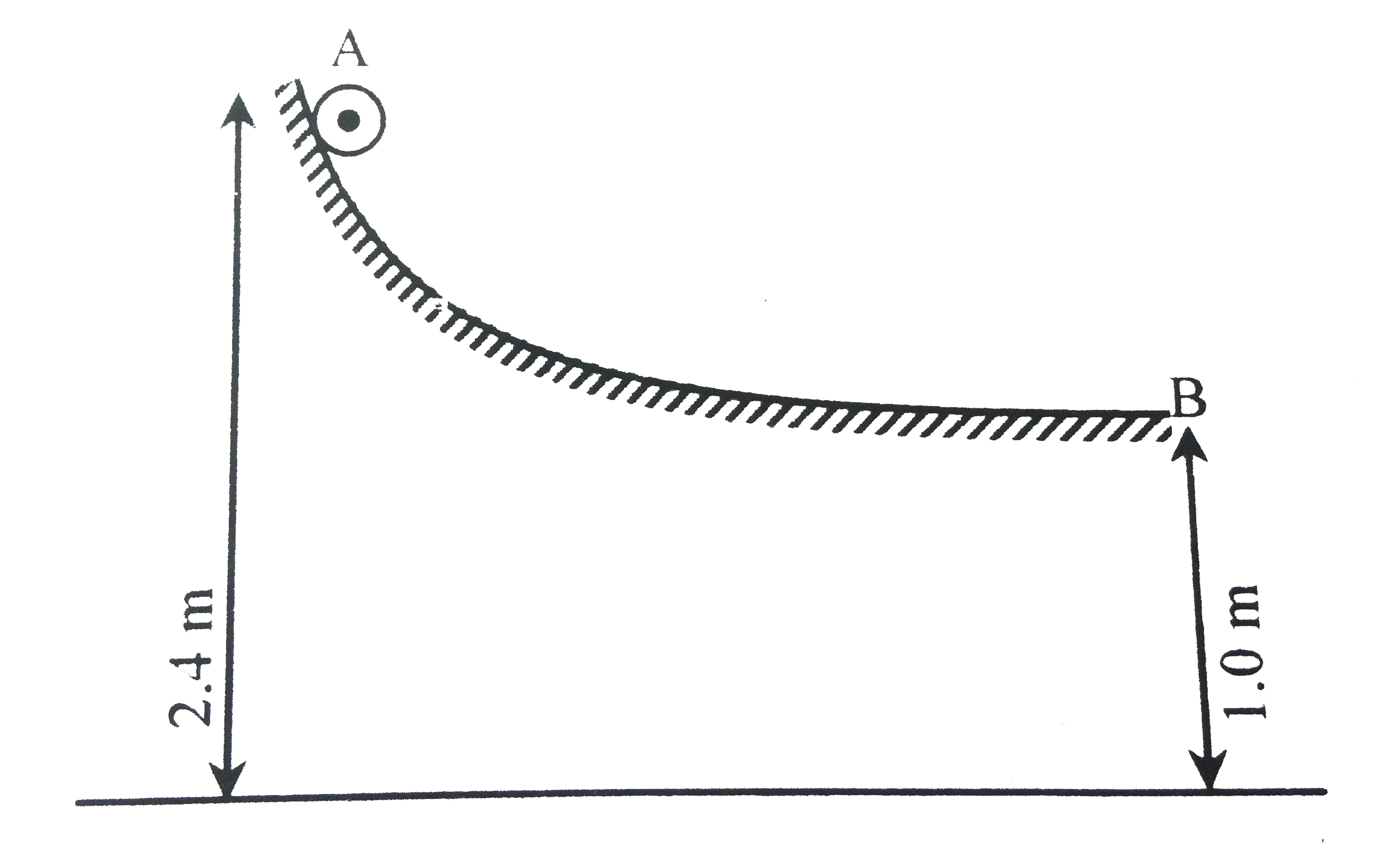
- A small sphere rolls down without slipping from the top of a track in ...
Text Solution
|
- A thin uniform bar lies on a frictionless horizonta surface and is fre...
Text Solution
|
- A block X of mass 0.5 kg is held by a long massless string on a fricti...
Text Solution
|
- Two thin circular discs sof mass 2 kg and radius 10 cm each are joined...
Text Solution
|
- Two heavy metallic plates are joined together at 90^@ to each other. A...
Text Solution
|
- A rectangular plate of mass M and dimension axxb is held in horizonta...
Text Solution
|
- A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as ...
Text Solution
|
- Four solid sphereas each of diameter sqrt(5) cm and mass 0.5 kg are pl...
Text Solution
|
- A lamina is made by removing a small disc of diameter 2R from a bigg...
Text Solution
|
- A uniform circular disc of mass 50 kg and radius 0.4 m is rotating wit...
Text Solution
|
- A uniform circular disc of mass 1.5 kg and raius 0.5 m is initially a...
Text Solution
|
- A horizontal circular platform of radius 0.5 m and mass axis. Two mass...
Text Solution
|
- Two identical uniform discs roll without slipping on tow different suf...
Text Solution
|
- The densitis of two solid spheres A and B of the same radii R very wit...
Text Solution
|
- A ring and a disc are initially at rest, side by side, at the top of a...
Text Solution
|
 .
. 