Home
Class 12
MATHS
Find the area of the region bounded by ...

Find the area of the region bounded by the curve `y^2= x`and the lines `x = 1, x = 4`and the x-axis.

Text Solution

Verified by Experts

`y^(2)=x` is a symmetric curve about X-axis. ABCDA is the region bounded by `x=1, x=4` and `y^(2)=x` and X-axis.

Required area `=` area of ABCDA
`=int_(1)^(4)|y|dx=int_(1)^(4)sqrt(x)dx`
`=[(x^(3//2))/(3//2)]_(1)^(4)=(2)/(3)[4^(3//2)-1^(3//2)]`
`=(2)/(3)(8-1)=(14)/(3)` sq. units.
Promotional Banner

Topper's Solved these Questions

  • APPLICATIONS OF INTEGRALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8.2|7 Videos

  • APPLICATIONS OF INTEGRALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|19 Videos

  • APPLICATIONS OF INTEGRALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8 C Questions For Competitive Examinations|10 Videos

  • APPLICATIONS OF DERIVATIVES

    NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|24 Videos

  • Continuity and Differentiability

    NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|23 Videos

Similar Questions

Explore conceptually related problems

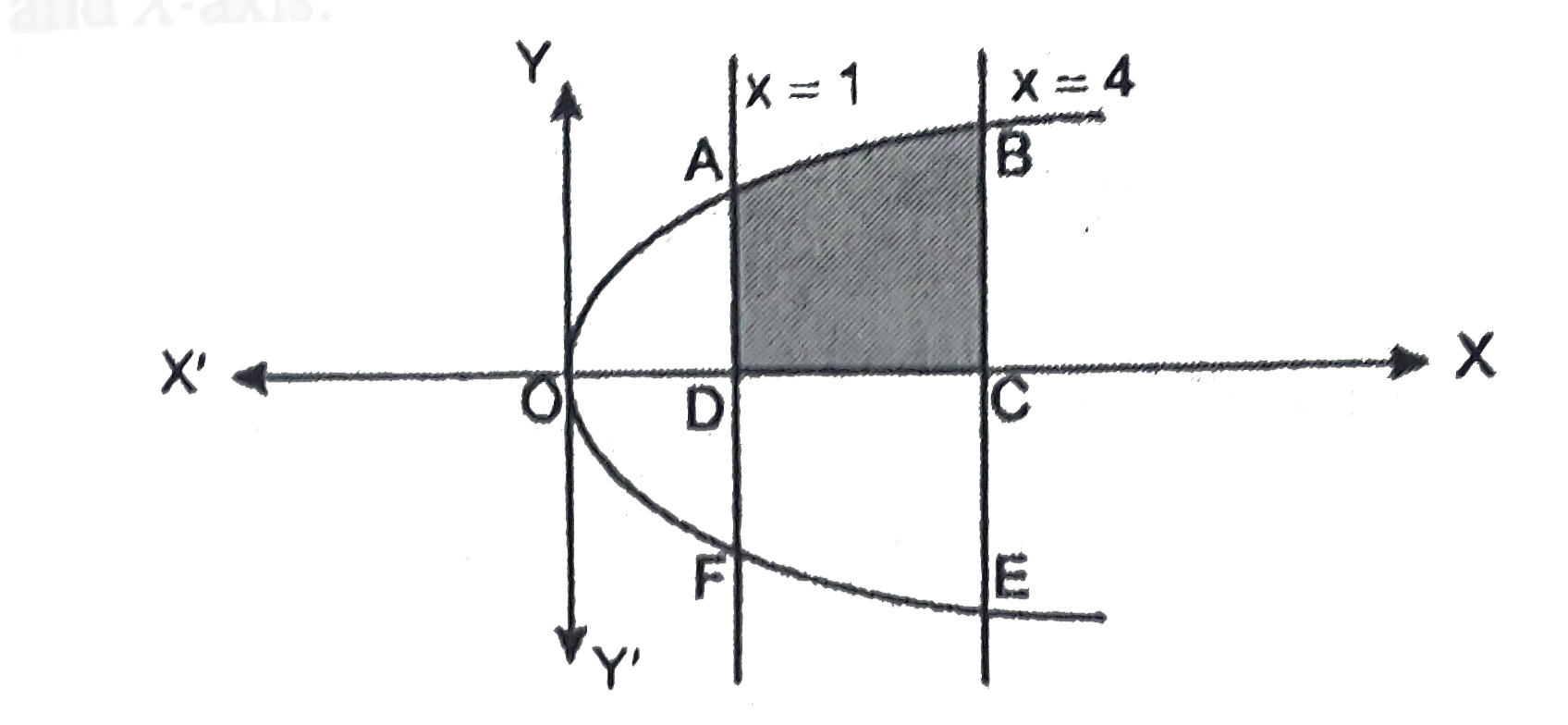
Find the area of the region bounded by the curve y^2=4x and the line x = 3 .

Find the area of the region bounded by the curve y=x^2 and the line y" "=" "4 .

The area of the region bounded by the curve y = x + 1 and the lines x=2, x=3, is

Find the area of the region bounded by the curve y=x^3 and the lines y = x + 6 and y =0.

Find the area of the region bounded by the curves x=4y-y^(2) and the Y-axis.

Find the area of the region bounded by the curves y=x^3 and the lines y=x+6 and y=0.

Find the area of the region bounded by the curves x=2y-y^2 and y=2+x .

Find the area of the region bounded by the curve y^(2)=4x" and " x^(2)=4y .

Find the area of the region bounded by the curve y^(2)=4x" and " x^(2)=4y .

The area of the region bounded by the curve y=x^(3) , X-axis and the ordinates x = 1, x = 4 is