Thales theorem is given by a greek mathe...

Thales theorem is given by a greek mathematician. According to this theorem, if a line is drawn parallel to one side of a triangle then it divides the other two sides in the same ratio. This theorem is also known as Basic Proportionality Theorem.

Here, the value of x is :

A

20 cm

B

15 cm

C

5 cm

D

10 cm

Text Solution

Verified by Experts

The correct Answer is:

A

Promotional Banner

Promotional Banner

Topper's Solved these Questions

SAMPLE PAPER 6
EDUCART PUBLICATION|Exercise SECTION C|10 Videos
SAMPLE PAPER 6
EDUCART PUBLICATION|Exercise SECTION- A|20 Videos
SAMPLE PAPER 6
EDUCART PUBLICATION|Exercise SECTION- C |10 Videos
SAMPLE PAPER 5
EDUCART PUBLICATION|Exercise PART - B (SECTION - V) |4 Videos
SAMPLE PAPER 7
EDUCART PUBLICATION|Exercise PART - B (SECTION - V) |8 Videos

Similar Questions

Explore conceptually related problems

Basic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.

Theorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

'If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.

If a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE||BC.

Theorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

Theorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.

Prove that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".

Theorem 6.6 : Lines which are parallel to the same line are parallel to each other.

EDUCART PUBLICATION-SAMPLE PAPER 6-SECTION B

The sum of two number is 25. One of the numbers exceeds the other by 9...
Text Solution
|
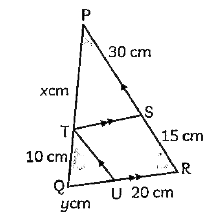
Calculate (x)/(y)
Text Solution
|
If Delta ABC ~ Delta DEF, such that angle A = 47 ^(@) and angle E = 83...
Text Solution
|
Find the value of (3-4 sin ^(2) A)/(4 cos ^(2) A -3) if sec A = (17)/...
Text Solution
|
Find the ratio of circumference of two circles whose areas are in the ...
Text Solution
|
Rita, Sita, Gita and Shyam are playing a bride game. It is four person...
Text Solution
|
Thales theorem is given by a greek mathematician. According to this th...
Text Solution
|
What is the probability of getting exactly one head, when two coins ar...
Text Solution
|
Find the number of solutions for the pair of equations x + 3y + 5 =0 a...
Text Solution
|
What is the smallest number by which (891)/(3500) must be multiplied s...
Text Solution
|
Find the side of a square whose diagonal is 10 cm.
Text Solution
|
An integer is 1 less than twice that of another. If their sum is 23 th...
Text Solution
|
What will be the number of the zero (s), if the graph of a quadratic p...
Text Solution
|
Evaluate the area of a semi-circle whose radius is 8.4 cm.
Text Solution
|
In Delta ABC, AD is the internal bisector of /A, meeting the side BC a...
Text Solution
|
Express R(3)interms of R(1) and R(2), where the sum of areas of two c...
Text Solution
|
Find the value of c in p (x) = ax ^(2) + bx + c, if one of the zeroes ...
Text Solution
|
A ladder 10 m log reaches the window of a house 8 m above the ground....
Text Solution
|
What is value of alpha + beta, if tan alpha =1 and sec beta = sqrt2 ?
Text Solution
|
What is the value of 'k', if one zero of the polynomial (k -1) x ^(2) ...
Text Solution
|