Home
Class 12
PHYSICS
Column I shows different sets of standin...

Column I shows different sets of standing waves in a string of length L whose ends are fixed or free according to respective figure and Column - II shows possible equations for them where symbols have usual meaning

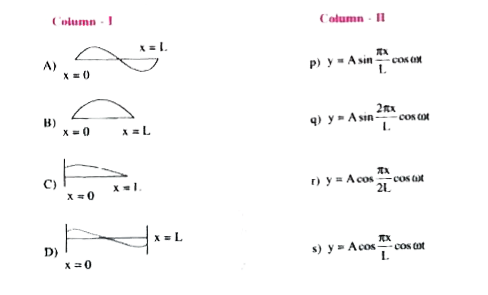
Text Solution

Verified by Experts

The correct Answer is:
A, B, C, D
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • WAVE MOTION

    AAKASH SERIES|Exercise PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)|10 Videos

  • WAVE MOTION

    AAKASH SERIES|Exercise PRACTICE SHEET ADVANCED (LINKED COMPREHENSION TYPE QUESTIONS)|9 Videos

  • UNITS AND MEASUREMENTS

    AAKASH SERIES|Exercise EXERCISE -3|66 Videos

  • WAVE MOTION AND SOUND

    AAKASH SERIES|Exercise PROBLEMS (LEVEL - II)|97 Videos

Similar Questions

Explore conceptually related problems

Draw a diagram to show the shape of a square wave pulse on a string when it gets reflected from (i) fixed boundary and (ii) a free end boundary.

Column-II lists some equations and arrangements of string. They are either corresponding to stationary wave or progressive wave match the entries of column-I with all possible entries in column-II

The wave-function for a certain standing wave on a string fixed at both ends is y(x,t) = 0.5 sin (0.025pix) cos500t where x and y are in centimeters and t is seconds. The shortest possible length of the string is :

Figure shows different standing wave patterns on a string of linear mass density 4.0 xx 10^-2 kg//m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m. (i) Obtain the frequencies of the modes shown in figures (a) and (b). (ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

String I and II have identical and linear mass densities, but string I is under greater tension than string II . The accompanying figure shows four different situations, A to D , in which standing wave patterns exist on the two strings. In which situation it is possible that strings I and II are oscillating at the same resonant frequency ?

A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm respectively. The minimum possible length of the string is:

Four pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are mu,4mu,9mu and 16mu , respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F . Find the time taken by wave to reach from source end to fixed end.

A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm, respectively. (a) What is the minimum possible length of the string? (b) If the tension is 10 N and the linear mass density is 4 g/m, what is the fundamental frequency?

A light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are mu and 9mu and the tension is T . Find the possible values of frequencies such that junction of two wire point A is a node.

A stationary wave of amplitude A is generated between the two fixed ends x = 0 and x = L. The particle at x=(L)/(3) is a node. There are only two particle between x =(L)/(6) and x=(L)/(3) which have maximum speed half of the maximum speed of the anti-node. Again there are only two particles between x= 0 and x=(L)/(6) which have maximum speed half of that at the antibodes. The slope of the wave function at x=(L)/(3) changes with respect to time according to the graph shown. The symbols mu, omega and A are having their usual meanings if used in calculations. The time period of oscillations of a particle is

Home
Profile