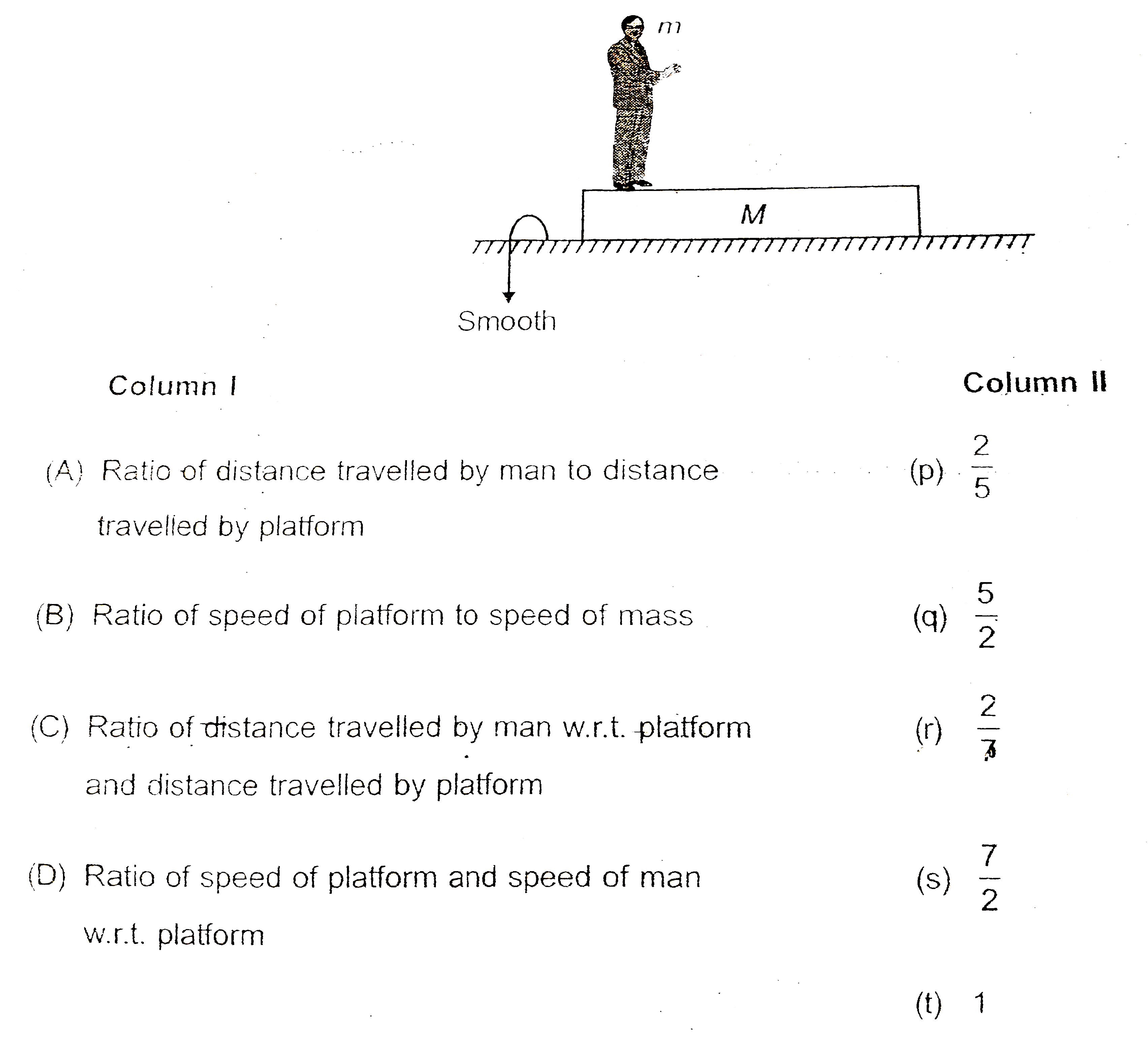Home
Class 12
PHYSICS
A man of mass m=2kg is standing on a pla...

A man of mass `m=2kg` is standing on a platform of mass `M=5kg`, then at any instant.

Answer

Step by step text solution for A man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant. by PHYSICS experts to help you in doubts & scoring excellent marks in Class 12 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTION

    AAKASH INSTITUTE|Exercise Assignment (Section - G) Integar Type Questions|9 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTION

    AAKASH INSTITUTE|Exercise Assignment (Section - H) Multiple True-False Type Questions|4 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTION

    AAKASH INSTITUTE|Exercise Assignment (Section - E) Assertion-Reason Type Questions|12 Videos

  • SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS

    AAKASH INSTITUTE|Exercise Assignment (Section-D (Assertion and reason))|5 Videos

  • TEST 1

    AAKASH INSTITUTE|Exercise EXERCISE|9 Videos

Similar Questions

Explore conceptually related problems

A man of mass m_1 = 80 kg is standing on a platform of mass m_2 = 20 kg that lies on a frictionless horizontal surface. The man starts moving on the platform with a velocity v_r = 10 m/s relative to the platform. Find the recoil speed of the platform.

A man of mass m_1 is standing on a platform of mass m_2 kept on a smooth horizontal surface. The man starts moving on the platform with a velocity v_r relative to the platform. Find the recoil velocity of platform.

Knowledge Check

  • A man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is

    A
    15.8 m
    B
    4.2 m
    C
    12.6 m
    D
    14.1 m

  • As shown in the figure, M is a man of mass 60 kg standing on a block of mass 40 kg kept on ground. The co-efficient of friction between the feet of the man and the block is 0.3 and that between B and the ground is 0.1. If the man accelerates with an acceleration 2(m)/(s^2) in the forward direction, then,

    A
    it is not possible
    B
    B will move backwards with an acceleration `0.5(m)/(s^2)`
    C
    B will not move
    D
    B will move forward with an acceleration `0.5(m)/(s^2)`.

    • Similar Questions

    Explore conceptually related problems

    A man of mass m_(1) is standing on a platform of mass m_(2) kept on a smooth horizontal surface. It the man moves a distance d w.r.t., the platform, find the displacement of the platform w.r.t., ground.

    A boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m//s at an angle of 45^@ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m//s^2 .

    A man of mass 60 kg is standing on a weighing machine (2) of mass 5kg placed on ground. Another identical weighing machine is placed over man’s head. A block of mass 50kg is put on the weighing machine (1) . Calculate the readings of weighing machines (1) and (2) .

    A man with mass 85 kg stands on a platform with mass 25 kg. He pulls on the free end of a rope that runs over a pulley on the ceiling and has its other end fastened to the platform. The mass of the rope and the mass of the pulley can be neglected, and the pulley is frictionless. With what force does he have to pull so that he and the platform have an upward acceleration of 2.2m/s^(2) . (Take g= 10m/s^(2) )

    A man of mass 75 kg is standing in an elevator which is moving with an acceleration of 5 m//s^2 in upward direction.The apparent weight of the man will be (g=10 m//s^2)

    A horizontal platform with a mass of 100 kg rotates at 10 (rpm) around a vertical axis passing through its centre. A man of mass 60 kg is standing on its edge. The platform begins to rotaté with an angular velocity omega (rpm) , if the man "moves from the edge of the platform to its centre. Regard the platform as a circular homogeneous disk and the man as a point mass. Find the value of (3 omega)/(11) .

    Home
    Profile