Home
Class 11
MATHS
In Figure, if P is (2, 4, 5), find the ...

In Figure, if P is (2, 4, 5), find the coordinates of F.

Text Solution

Verified by Experts

Given ,
`p(2,4,3)`
So, `x=2, y=4 , z=5`
Point F lies in XZ plane.
...
Promotional Banner

Topper's Solved these Questions

  • INTRODUCTION TO THREE DIMENSIONAL GEOMETRY

    NCERT|Exercise MISCELLANEOUS EXERCISE|6 Videos

  • INTRODUCTION TO THREE DIMENSIONAL GEOMETRY

    NCERT|Exercise EXERCISE 12.1|4 Videos

  • INTRODUCTION TO THREE DIMENSIONAL GEOMETRY

    NCERT|Exercise EXERCISE 12.2|5 Videos

  • CONIC SECTIONS

    NCERT|Exercise EXERCISE 11.1|15 Videos

  • LIMITS AND DERIVATIVES

    NCERT|Exercise EXERCISE 13.3|8 Videos

Similar Questions

Explore conceptually related problems

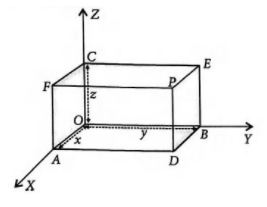
In the figure of Ex 1 if p is (2,4,5) find the co- ordinates of E

PP' is a focal chord of the parabola y^(2)=8x . If the coordinates of P are (18,12), find the coordinates of P'

The x-coordinate of a point P is twice its y- coordinate.If P is equidistant from Q(2,-5) and R(-3,6), then find the coordinates of P.

If P(-2,-5) and Q(4,3) and point R divides the segment PQ is the ratio 3:4 then find the coordinates of points R.

In the following figure, if the coordinates of P are (a,b,c) then the coordinates of A,B and C are respectively

A line intersects the y-axis and x-axis at the points P and Q respectively.If (2,5) is the mid- point of PQ ,then find the coordinates of P and Q.

The x-coordinate of a point P is twice its y-coordinate. If P equisdtant from Q(2,-5) and R(3,6) find the coordinates of P .

If the origin is shifted to the point (2,3) the coordinates of a point become (5,-4). Find the original coordinates, which the axes are parallel.

* Let P and Q be the points of trisection of the line segment joining the points A(2,-2) and B(-7,4) such that P is nearer to A .Find the coordinates of P and Q.

If the coordinates of points A and B are (-2, -2) and (2, -4) respectively, find the coordinates of the point P such that AP = (3)/(7)AB , where P lies on the line segment AB.