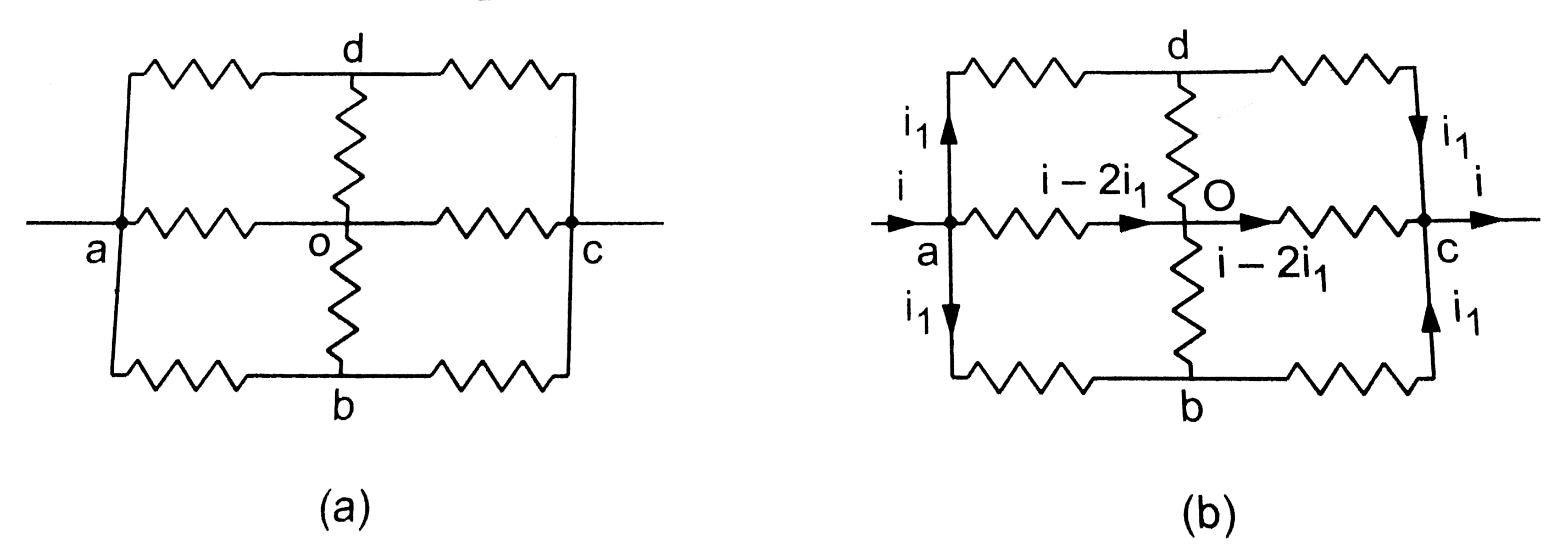Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CURRENT IN CONDUCTORS
HC VERMA|Exercise Short Answer|17 VideosELECTRIC CURRENT IN CONDUCTORS
HC VERMA|Exercise Objective 1|16 VideosELECTRIC CURRENT IN CONDUCTORS
HC VERMA|Exercise Worked Out Examples|32 VideosDISPERSION AND SPECTRA
HC VERMA|Exercise Exercises|11 VideosELECTRIC CURRENT THROUGH GASES
HC VERMA|Exercise Exercises|23 Videos
Similar Questions
Explore conceptually related problems