(a)
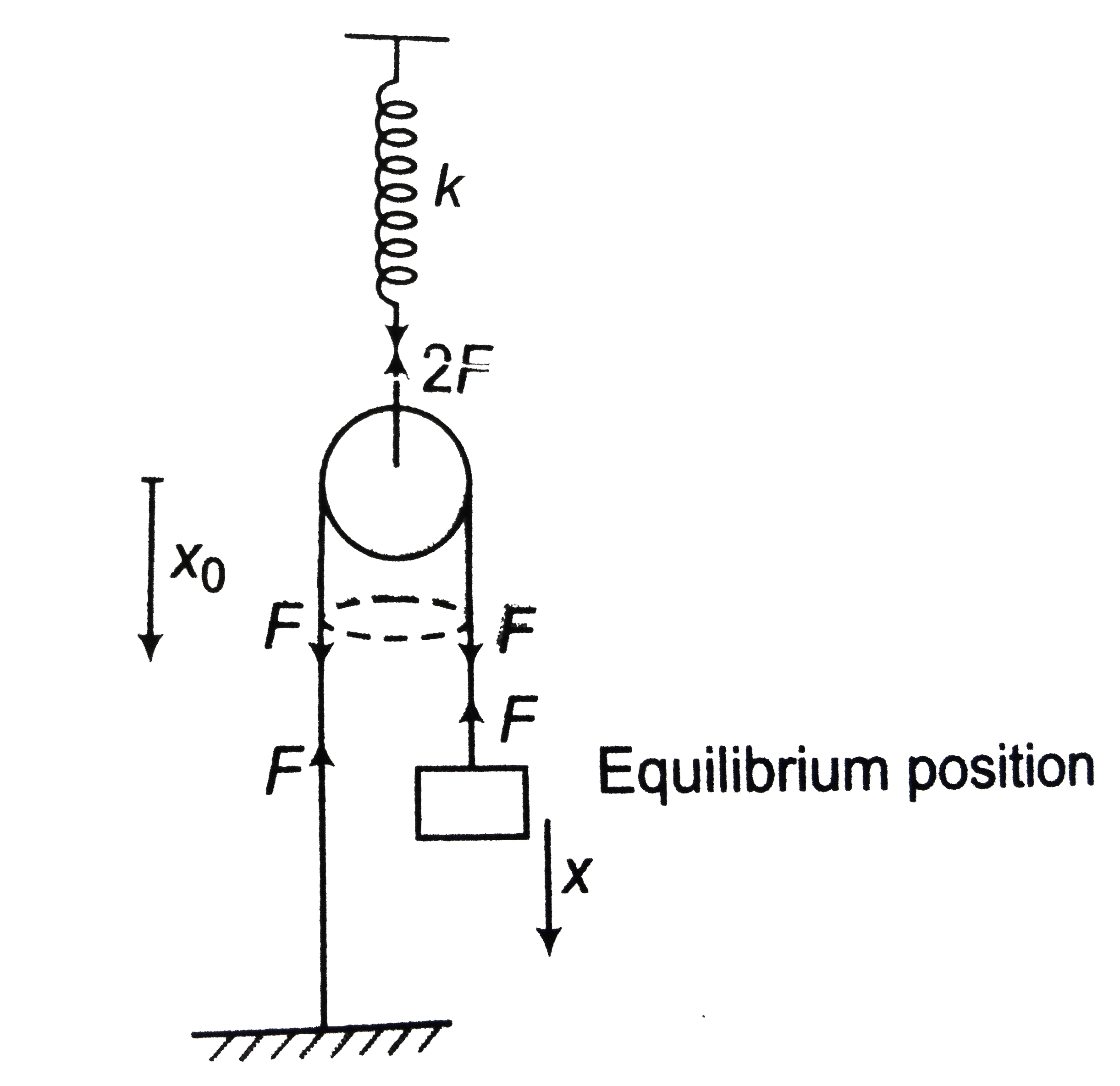
Two force are acting on the block :
(i) weight
(ii) tension
Weight is a constant force which does not contribute in time period. Tension is a variable force. Let tension increases by `F` when displaced from the equilibrium position by `x`. This increase in tension is the change in variable force. So, this is also the net restoring force. The distribution of this increase in tension `F` is as shown in figure.
Spring gets an extra stretching force `2F`. Let `x_(0)` is the extra extension in the spring by this extra force `2F`. Then,
`2F = kx_(0)`
or `x_(0) = (2F)/(k)`
Now, we can see that by this extra extension of spring, pulley will also come by the same distance `x_(0)` and
`x = 2x_(0) = 2((2F)/(k))`
`rArr F = (k)/(4)x`
But `F` is also the net restoring force on block. So, we can write
`F = - ((k)/(4))x`
`:. T = 2pi sqrt((m)/(k//4)) (as k_(e) = k//4)`
` = 2pi sqrt((4m)/(k))`
(b) Using the same concepts as discussed above,
`(F)/(2) = kx_(0)`
or `x_(0) = (F)/(2k)`
But this time,
`x_(0)` = extra extension on spring.
= extra increase in length ABCD
` = 2x`
or `(F)/(2k) = 2x`
or `F = 4kx`
Due to the restoring nature of `F` we can write,
`F = - (4k)x`
`:. T = 2pi sqrt((m)/(4k)) (as k_(e) = 4k)`

.


 .
.