Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS-2
CENGAGE PHYSICS|Exercise Exercise 5.1|15 VideosKINEMATICS-2
CENGAGE PHYSICS|Exercise Exercise 5.2|25 VideosKINEMATICS-2
CENGAGE PHYSICS|Exercise Exercise Integer|9 VideosKINEMATICS-1
CENGAGE PHYSICS|Exercise Integer|9 VideosKINETIC THEORY OF GASES
CENGAGE PHYSICS|Exercise Compression|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-KINEMATICS-2-Solved Examples
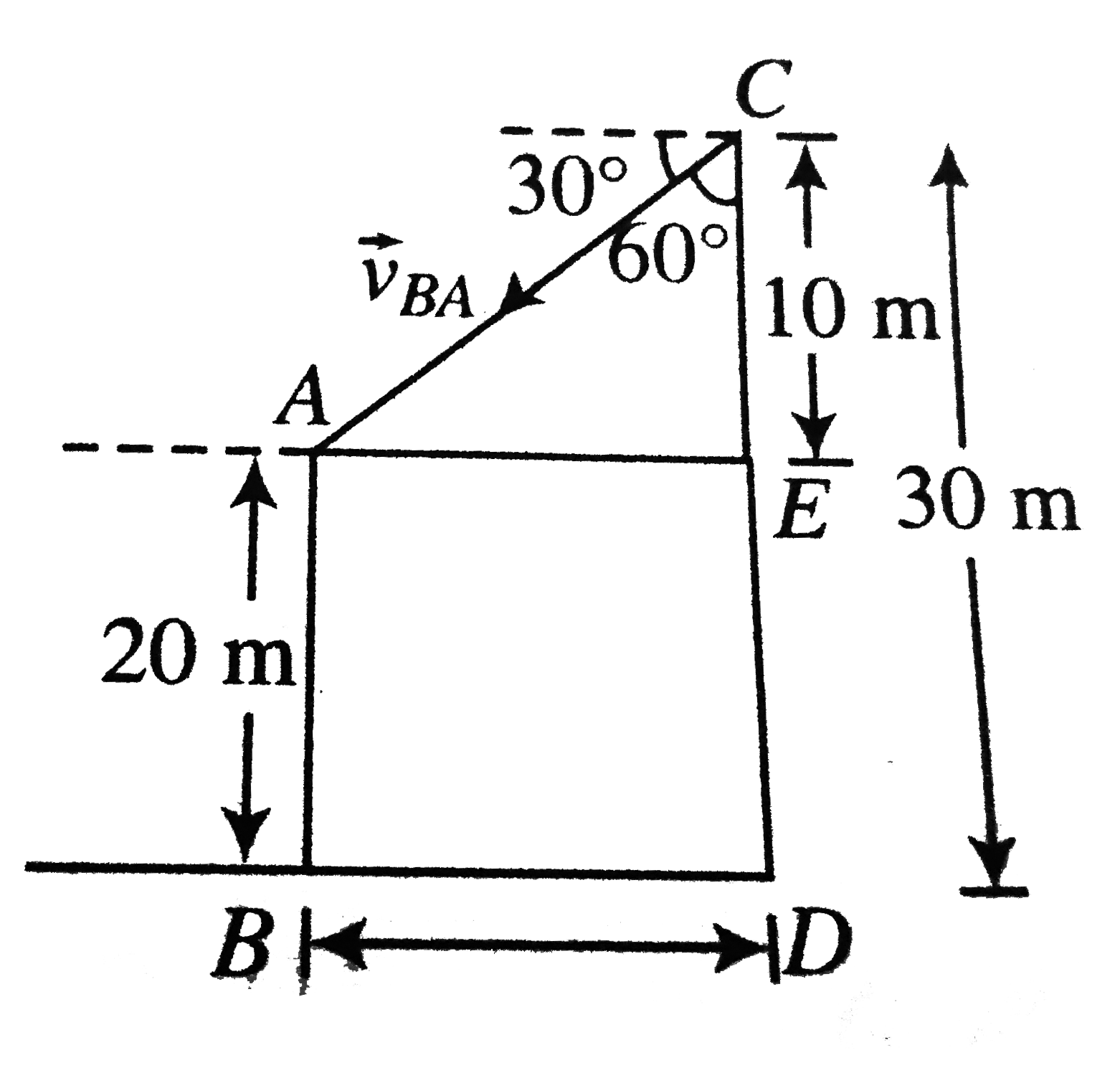
- Two towers AB and CD are situated at a distance d apart, as shown in ...
Text Solution
|
- Two guns situated at the top of a hill of height 10 m fire one shot ea...
Text Solution
|
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
- On a frictionless horizontal surface , assumed to be the x-y plane ,...
Text Solution
|
- An aircraft is .flying. horizontally with a constant vefocity =200m//s...
Text Solution
|
- The current velocity of river grows in proportion to the distance from...
Text Solution
|
- Three particles A, B and C are situated at the vertices of an equilate...
Text Solution
|

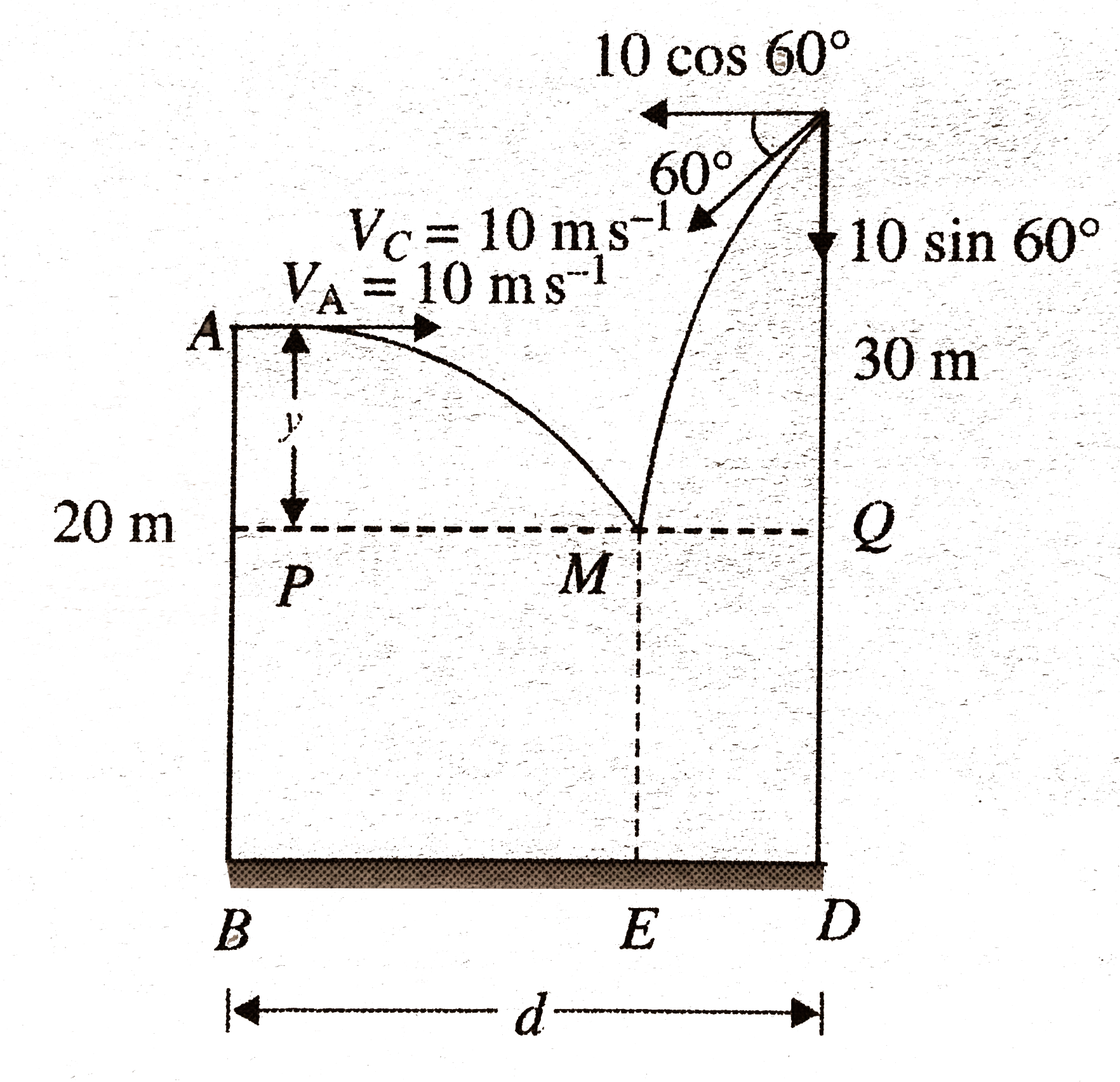 ,
,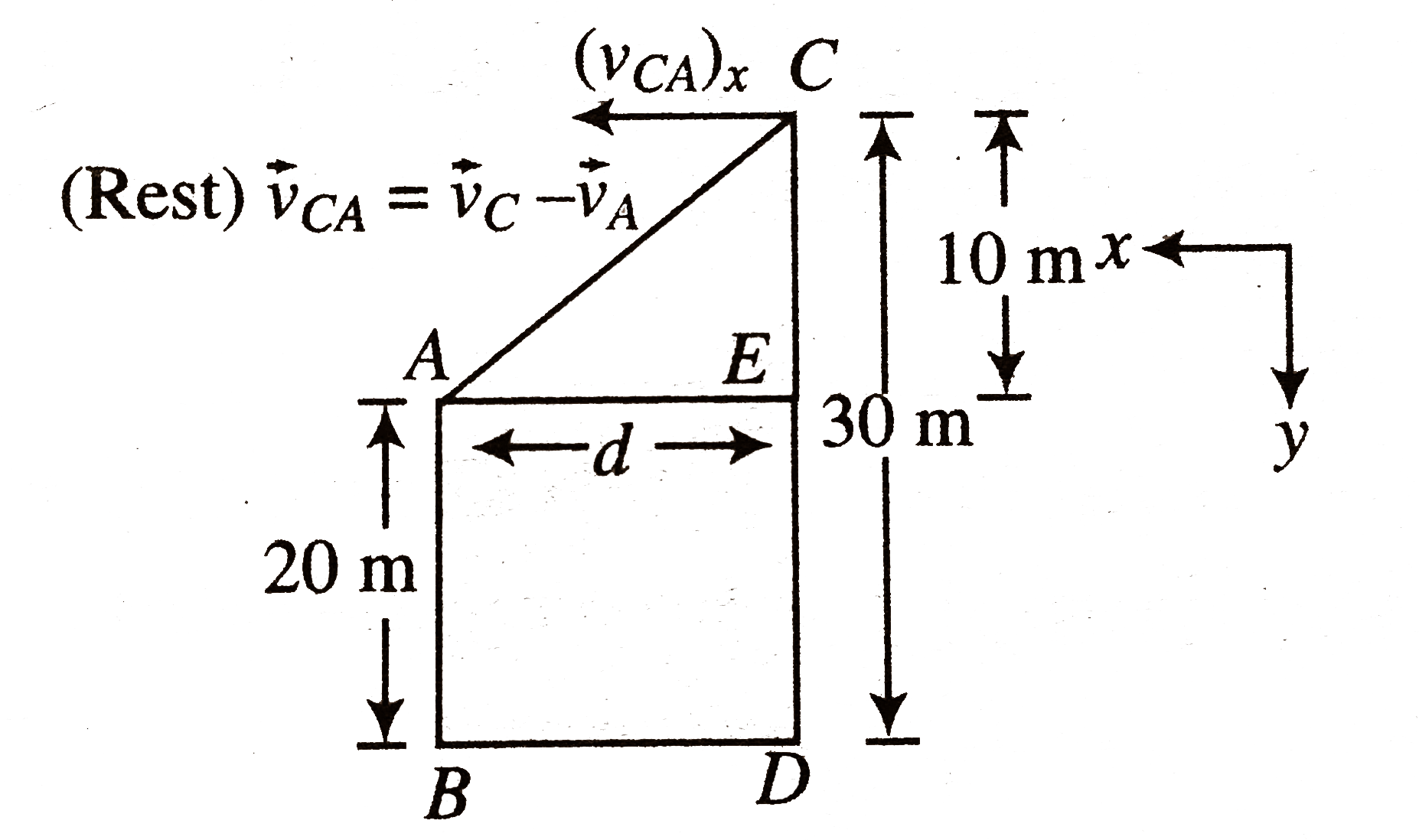 ,
,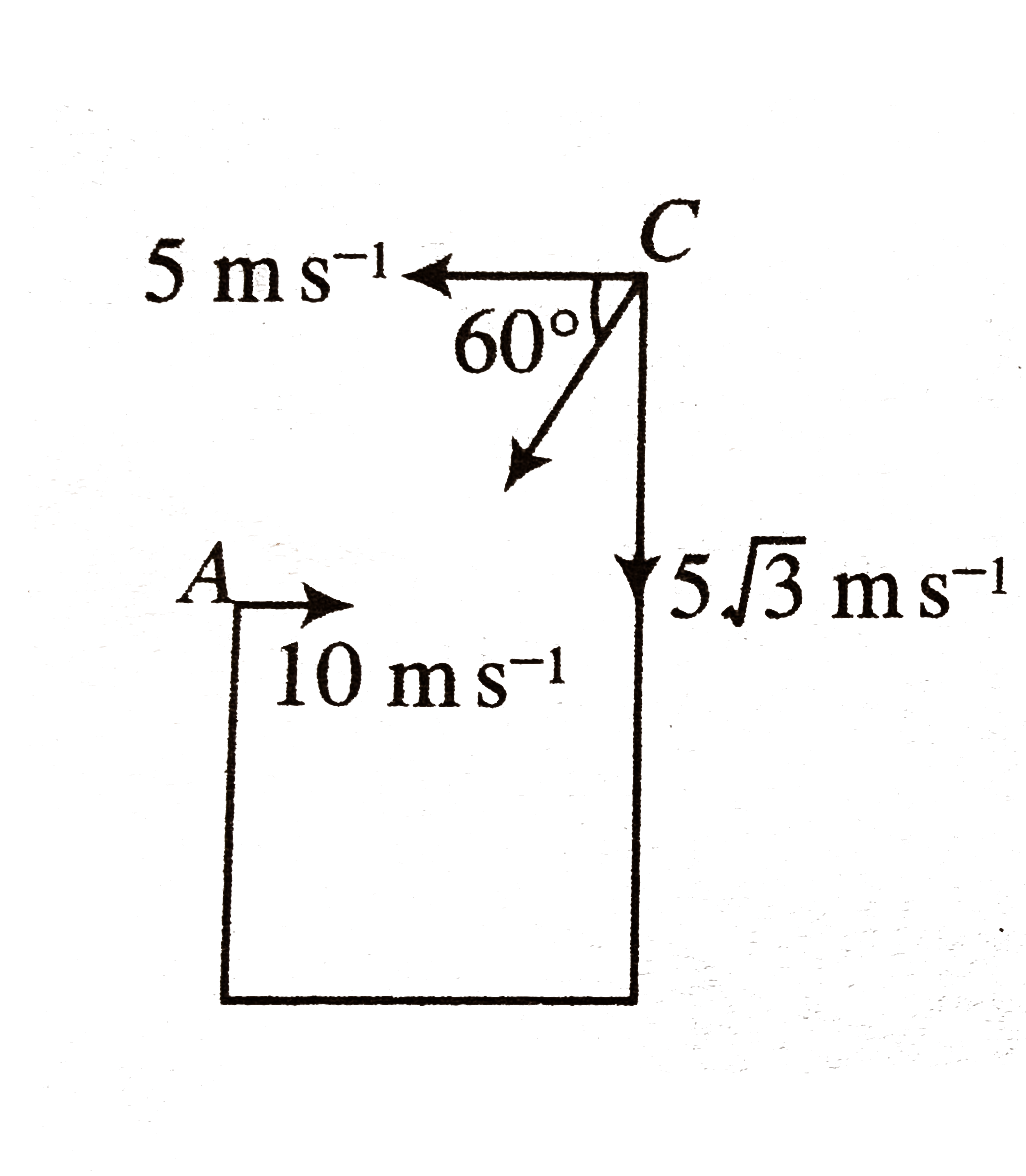 ,
, .
.