Text Solution
Verified by Experts
Topper's Solved these Questions
FLUID MECHANICS
CENGAGE PHYSICS|Exercise Exercise 4.3|10 VideosFLUID MECHANICS
CENGAGE PHYSICS|Exercise Exercise 4.4|10 VideosFLUID MECHANICS
CENGAGE PHYSICS|Exercise Exercise 4.1|11 VideosDIMENSIONS & MEASUREMENT
CENGAGE PHYSICS|Exercise Integer|2 VideosGRAVITATION
CENGAGE PHYSICS|Exercise INTEGER_TYPE|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-FLUID MECHANICS-Exercise 4.2
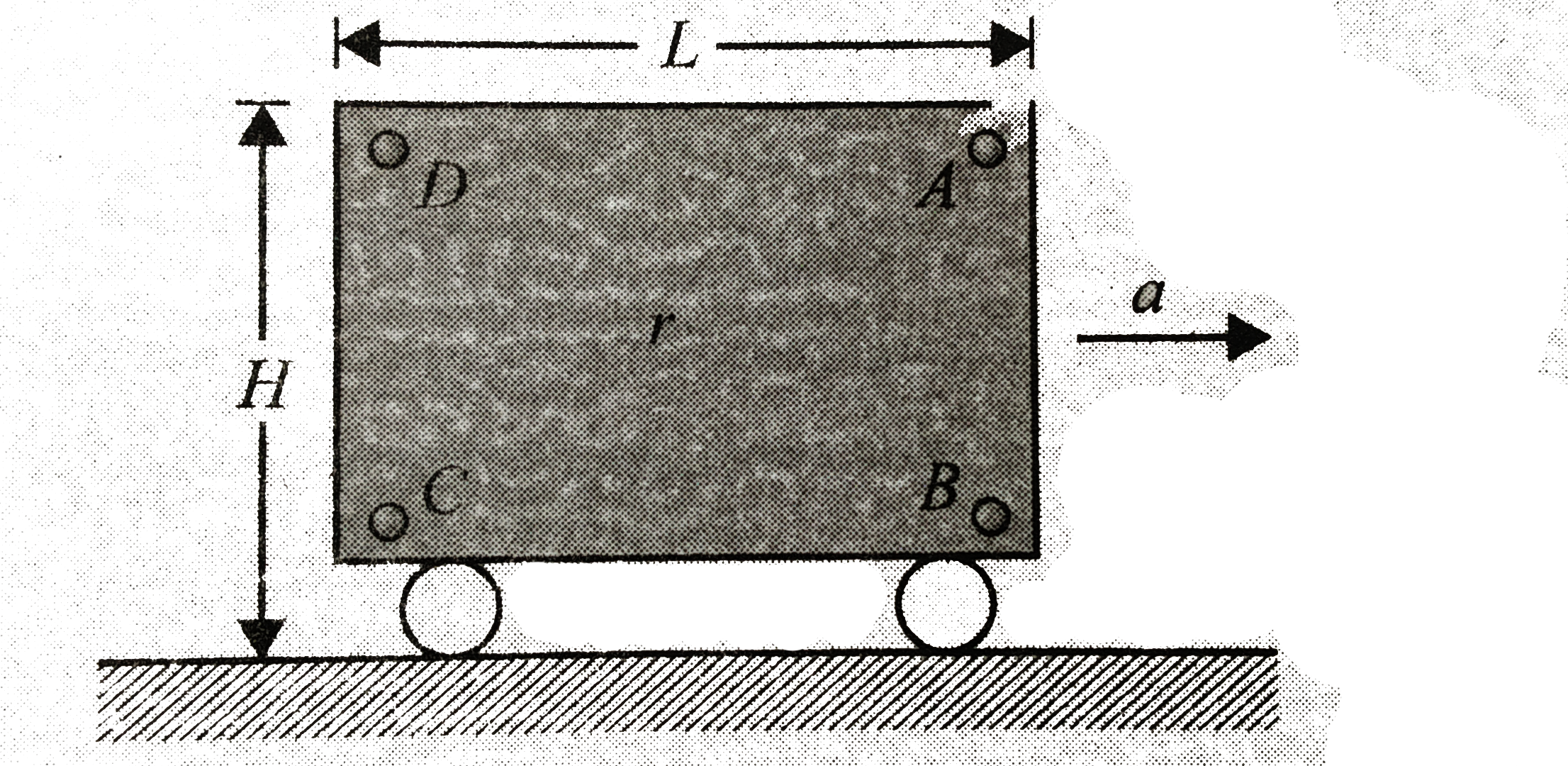
- A rectangular box is completely filled with a liquid of density rho, a...
Text Solution
|
- Figure shows an L-shaped tube tilled with a liquid to a height H. What...
Text Solution
|
- A barometer kept in an elevator accelerating upward reads 76 cm. The a...
Text Solution
|
- A barometer kept in an elevator reads 76 cm when it is at rest. If the...
Text Solution
|
- A container shown in Fig. is accelerated horizontally with acceleratio...
Text Solution
|
- A closed rectangular tank 10 m long, 5 m wide and 3 m deep is complete...
Text Solution
|
- A trolley containing a liquid slides down a smooth inclined plane of a...
Text Solution
|
- A cylinder of radius R and height H is foam unknown height h. When is ...
Text Solution
|
- A cylinder of radius R = 1 m and height H = 3 m two- thirds filled wit...
Text Solution
|
- A U- tube shown in Fig. containing two liquids of specific gravities r...
Text Solution
|
- A U tube is rotated about one of it's limbs with an angular velocity o...
Text Solution
|