A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ROTATIONAL DYNAMICS
A2Z|Exercise Assertion Reasoning|20 VideosROTATIONAL DYNAMICS
A2Z|Exercise NEET Questions|59 VideosROTATIONAL DYNAMICS
A2Z|Exercise Rotation And Translation Combined And Rolling Motion|18 VideosPROPERTIES OF MATTER
A2Z|Exercise Chapter Test|29 VideosTHERMAL PROPERTIES OF MATTER
A2Z|Exercise Chapter Test|30 Videos
Similar Questions
Explore conceptually related problems
A2Z-ROTATIONAL DYNAMICS-Problems Based On Mixed Concepts
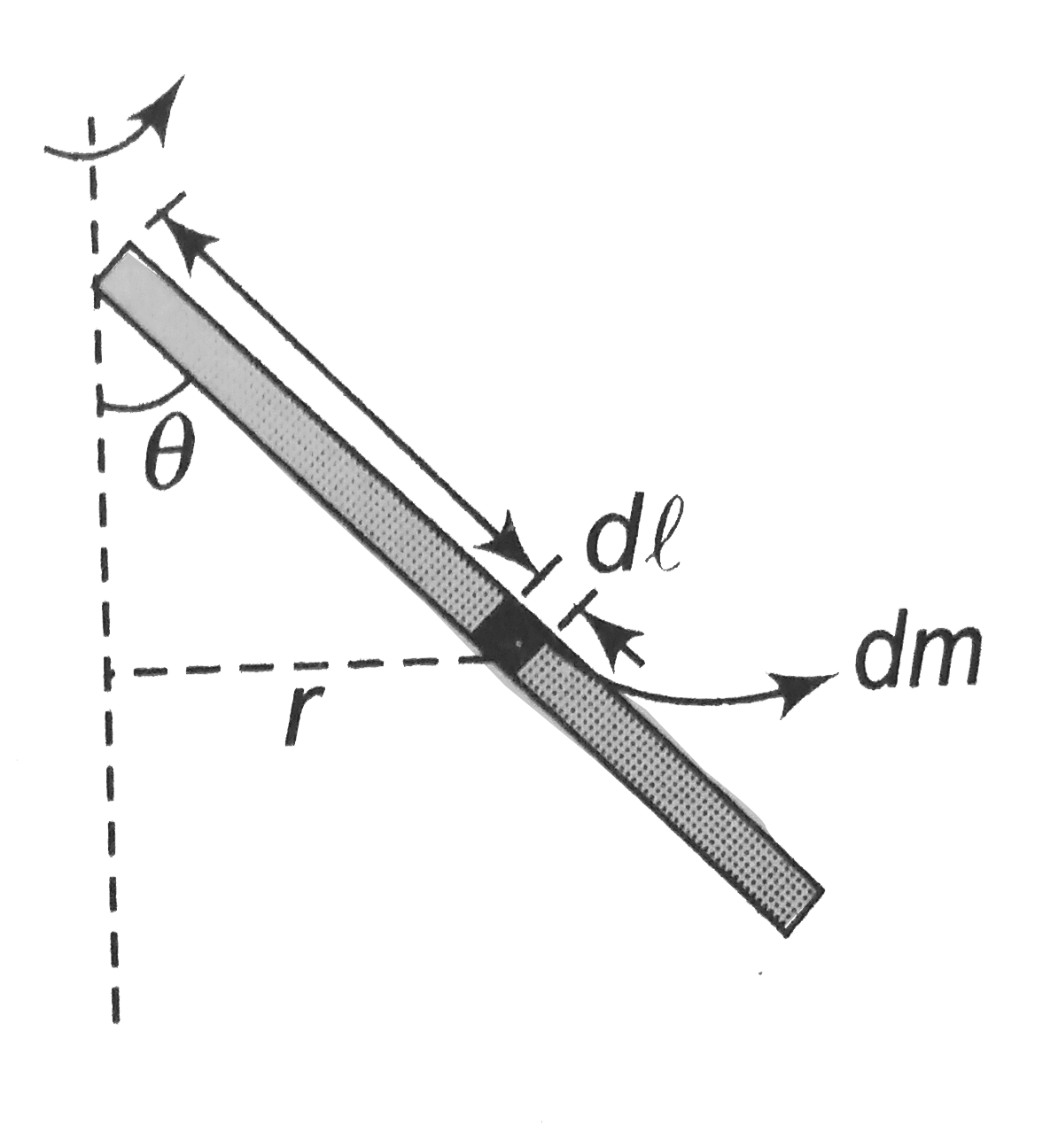
- A uniform rod of mass m and length l(0) is rotating with a constant an...
Text Solution
|
- Two points A and B on a disc have velocities v1 and v2, respectively, ...
Text Solution
|
- Two steel ball of equal diameter are connected by a rigid bar of negli...
Text Solution
|
- A brick of length L is placed on the horizontal floor. The bricks of s...
Text Solution
|
- A car moves with speed v on a horizontal circular track of radius R. A...
Text Solution
|
- A thin horizontal uniform rod AB of mass m and length l can rotate fre...
Text Solution
|
- A uniform disc of mass m is fitted (pivoted smoothly) with a rod of ma...
Text Solution
|
- The two uniform discs rotate separately on parallel axles. The upper d...
Text Solution
|
- A sphere of mass M and radius r shown in figure slips on a rough horiz...
Text Solution
|
- A wheel of mass 5 kg and radius 0.40 m is rolling on a road without sl...
Text Solution
|
- The moments of inertia of two rotating bodies A and are IA and IB(IA g...
Text Solution
|
- A body is rolling down an inclined plane. If kinetic energy of rotatio...
Text Solution
|
- A ring of radius R is rotating with an angular speed omega0 about a ho...
Text Solution
|
- A uniform solid sphere of radius r = ( R)/(5) is placed on the inside ...
Text Solution
|
- Average torque on a projectile of mass m (initial speed u and angle of...
Text Solution
|
- A car weighs 1800 kg. The distance between its front and back axles is...
Text Solution
|
- A track is mounted on a large wheel that is free to turn with neigligi...
Text Solution
|
- A sphere of mass M rolls without slipping on rough surface with centre...
Text Solution
|
- Figure shows two identical particles 1 and 2, each of mass m, moving i...
Text Solution
|
- A cylindrical rod of mass M, length L and radius R has two cords wound...
Text Solution
|
 .
.