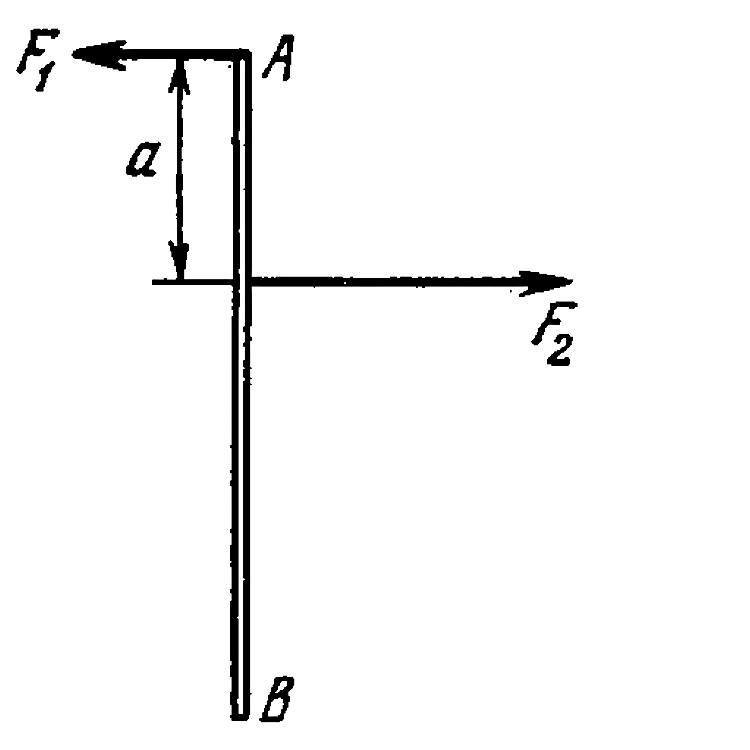Text Solution
Verified by Experts
Topper's Solved these Questions
PHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Elastic Deformation Of Asolid Body|25 VideosPHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Hydrodynamics|25 VideosPHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Universal Gravitation|34 VideosOSCILLATIONS AND WAVES
IE IRODOV, LA SENA & SS KROTOV|Exercise Electromagnetic Waves, Radiation|36 VideosTHERMODYNAMICS AND MOLECULAR PHYSICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Transport Phenomena|38 Videos
Similar Questions
Explore conceptually related problems
IE IRODOV, LA SENA & SS KROTOV-PHYSICAL FUNDAMENTALS OF MECHANICS-Dynamics Of A Solid Body
- A thin uniform rod AB of mass m=1.0kg moves translationally with accel...
Text Solution
|
- A force F=Ai+Bj is applied to a point whose radius vector relative to ...
Text Solution
|
- A force F1=Aj is applied to a point whose radius vector r1=ai, while a...
Text Solution
|
- Three forces are applied to a square plate as shown in Figure. Find th...
Text Solution
|
- Find the moment of inertia (a) of a thin uniform rod relative to the...
Text Solution
|
- Calculate the moment of inertia (a) of a copper uniform disc relativ...
Text Solution
|
- Demonstrate that in the case of a thin plate of arbitrary shape there ...
Text Solution
|
- A uniform disc of radius R=20cm has a round cut as shown in figure. Th...
Text Solution
|
- Using the formula for the moment of inertia of a uniform sphere, find ...
Text Solution
|
- A light thread with a body of mass m tied to its end is wound on a uni...
Text Solution
|
- The ends of thin threads tightly wound on the axle of radius r of the ...
Text Solution
|
- A thin horizontal uniform rod AB of mass m and length l can rotate fre...
Text Solution
|
- In the arrangement shown in figure the mass of the uniform solid cylin...
Text Solution
|
- In the system shown in figure the masses of the bodies are known to be...
Text Solution
|
- A uniform cylinder of radius R is spinned about it axis to the angular...
Text Solution
|
- A uniform disc of radius R is spinned to the angular velocity omega an...
Text Solution
|
- A flywheel with the initial angular velocity omega0 decelerates due to...
Text Solution
|
- A uniform cylinder of radius r and mass m can rotate freely about a fi...
Text Solution
|
- A uniform sphere of mass m and radius R rolls without slipping down an...
Text Solution
|
- A uniform cylinder of mass m and radius R starts descending at a momen...
Text Solution
|