Home
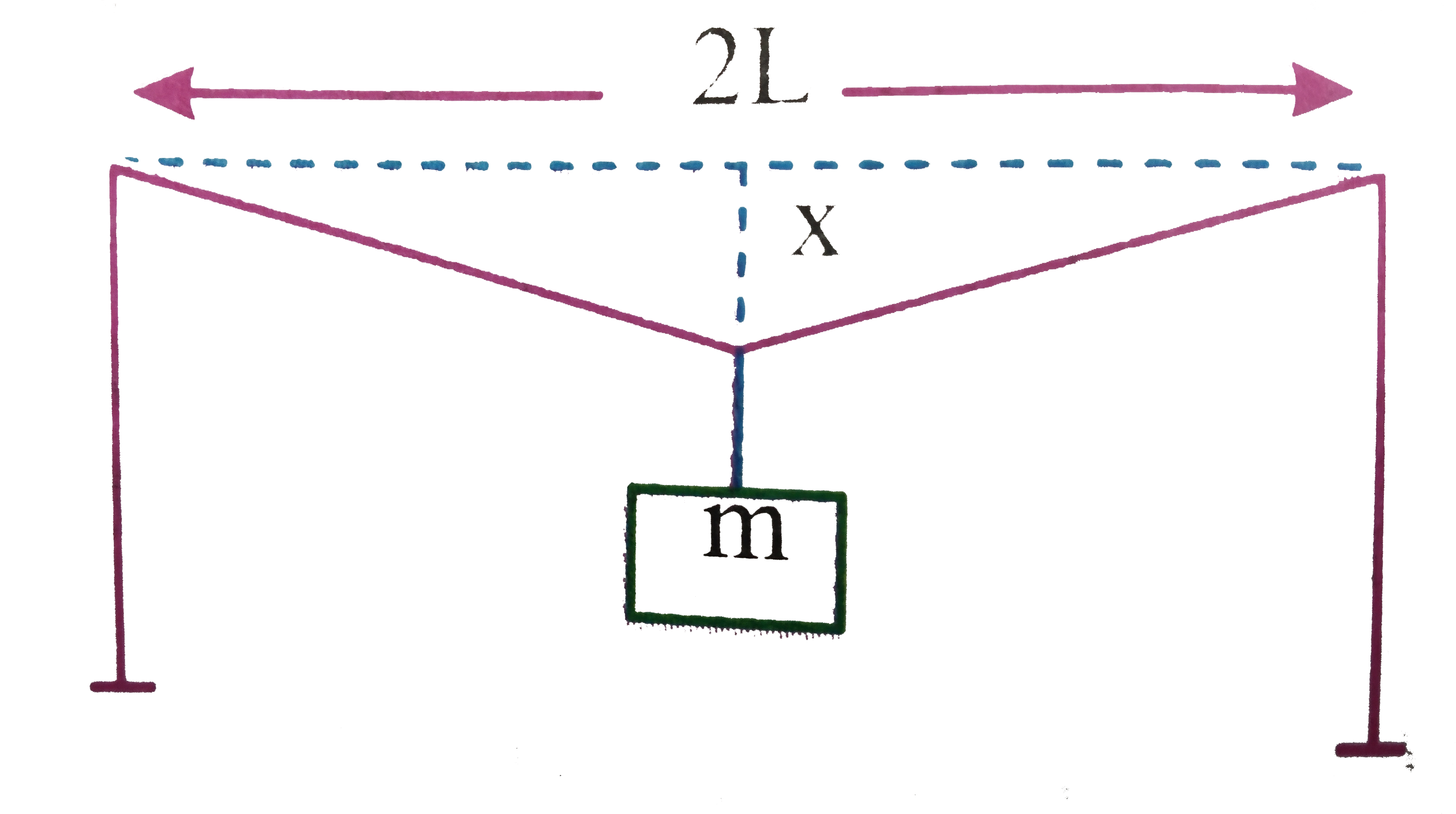
Class 11
PHYSICS
A mild steel wire of length 1.0m and cro...

A mild steel wire of length `1.0m` and cross sectional area `2L` is strethched, within its elastic limit horizontally between two pillars(figure). A mass of `m` is suspended form the midpont of the wire. Strain in the wire is

A

`(y^2)/(l)`

B

`(y^2)/(3l)`

C

`(y^2)/(4l)`

D

`(2y^2)/(l)`

Text Solution

Verified by Experts

The correct Answer is:
A
`Delta l = 2(y^(2) + l^(2))^(1//2) - 2l = 2l (1 + (y^(2))/(l^(2)))^(1//2) - 2l`
`= 2l (1 + (1)/(2) (y^(2))/(l^(2)))-2l = (y^(2))/(2l^(2)) xx 2l = (y^(2))/(l)`
energy `(1)/(2) xx (Y A Delta l^(2))/(2l) - 2l = (1)/(2) "stress" xx "strain" xx "volime"`
`= (1)/(2)y ("strain")^(2) A(2l) = (1)/(2) y((Delta l)/(2l))^(2) A.2l = (yA(Delta l)^(2))/(4l)`
Promotional Banner

Topper's Solved these Questions

  • MECHANICAL PROPERTIES OF SOLIDS

    NARAYNA|Exercise Comprehension-3:|2 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    NARAYNA|Exercise Comprehension-4:|3 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    NARAYNA|Exercise Comprehension-1:|2 Videos

  • MECHANICAL PROPERTIES OF FLUIDS

    NARAYNA|Exercise EXERCISE - III|30 Videos

  • MOTION IN A PLANE

    NARAYNA|Exercise Level-II(H.W)|31 Videos

Similar Questions

Explore conceptually related problems

A mild steel wire of length 1.0m and cross sectional area 5.0xx10^(-2)cm^(2) is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Y_("steel) = 200GPa)

A mild steel wire of length 1.0 m and cross-sectional are 0.5 xx 10^(-20)cm^(2) is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point. g = 10ms^(-2), Y=2 xx 10^(11)Nm^(-2 .

A steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is X. Strain in the wire is proportional to

A metal wire of length L_1 and area of cross section A is ttached to a rigid support. Another metal wire of length L_2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y_1 and Y_2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is

A steel wire having cross-sectional area 2 mm^(2) is stretched by 20 N. Find the lateral strain produced in the wire

A steel wire of diameter d=1.0mm is stretched horizontally between two clamps located at the distance l=2.0m from each other. A weight of mass m=0.25kg is suspended from the mid-point O of the wire. What will the resulting descent of the point O be in centrimetres?