A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression `2x_(0)` an block is released from rest. Collision with the wall `PQ` are elastic.

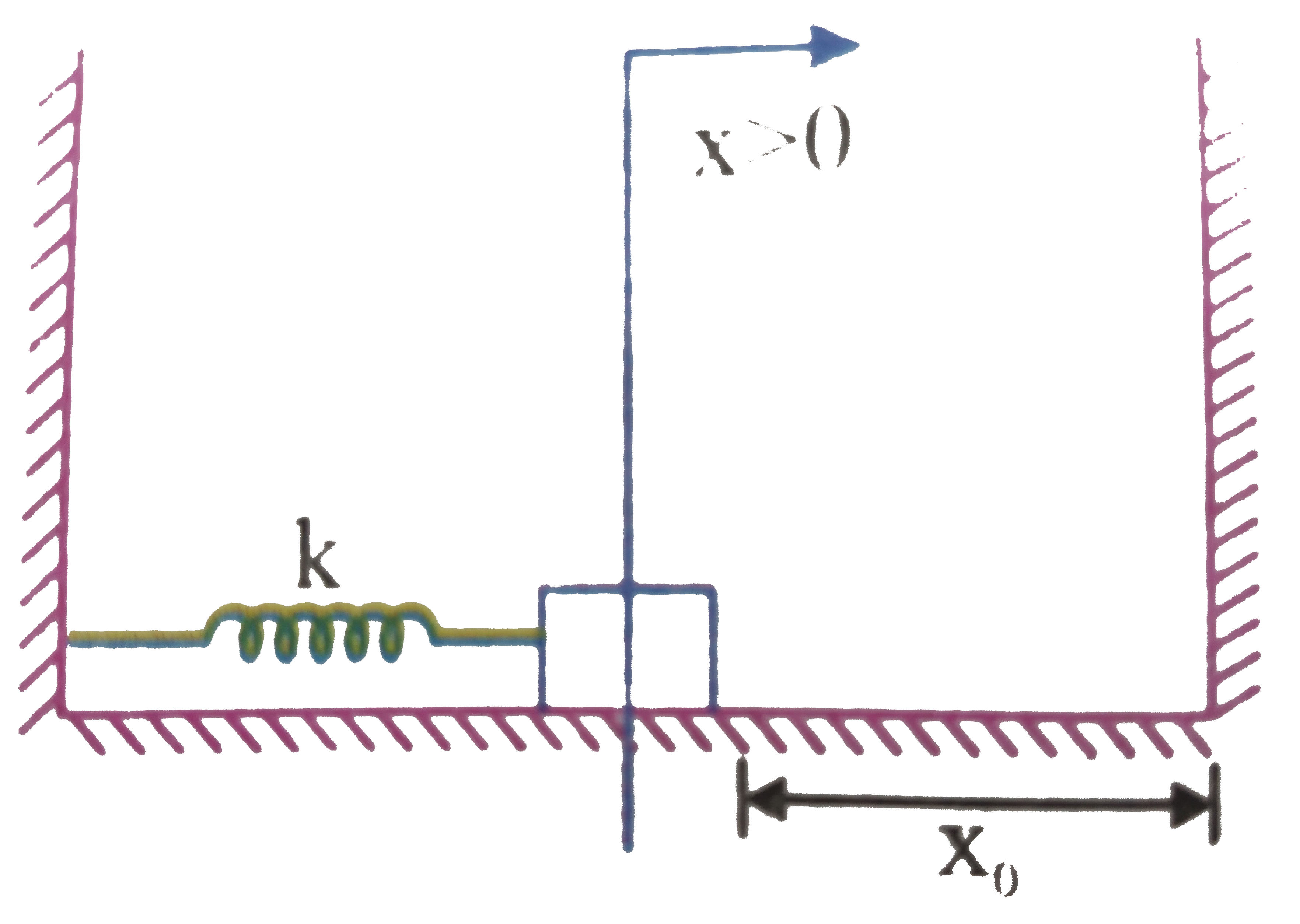
Find the time period of motion of the block:

Options

A. `(2pi)/(3) sqrt((m)/(k))`
B. `(4pi)/(3)sqrt((m)/(k))`
C. `(3pi)/(2)sqrt((m)/(k))`
D. `(pi)/(2)sqrt((m)/(k))`

Answer

B

Explanation

A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an intial compression `2x_(0)`and block is released form rest. Collisions with the wall `PQ` are elastic.

Treat initial position of block as origin `O`. Had wall not been...motion would have been normal `S.H.M.` with amplitude `2x_(0)` say............point, Given `A` and `b`

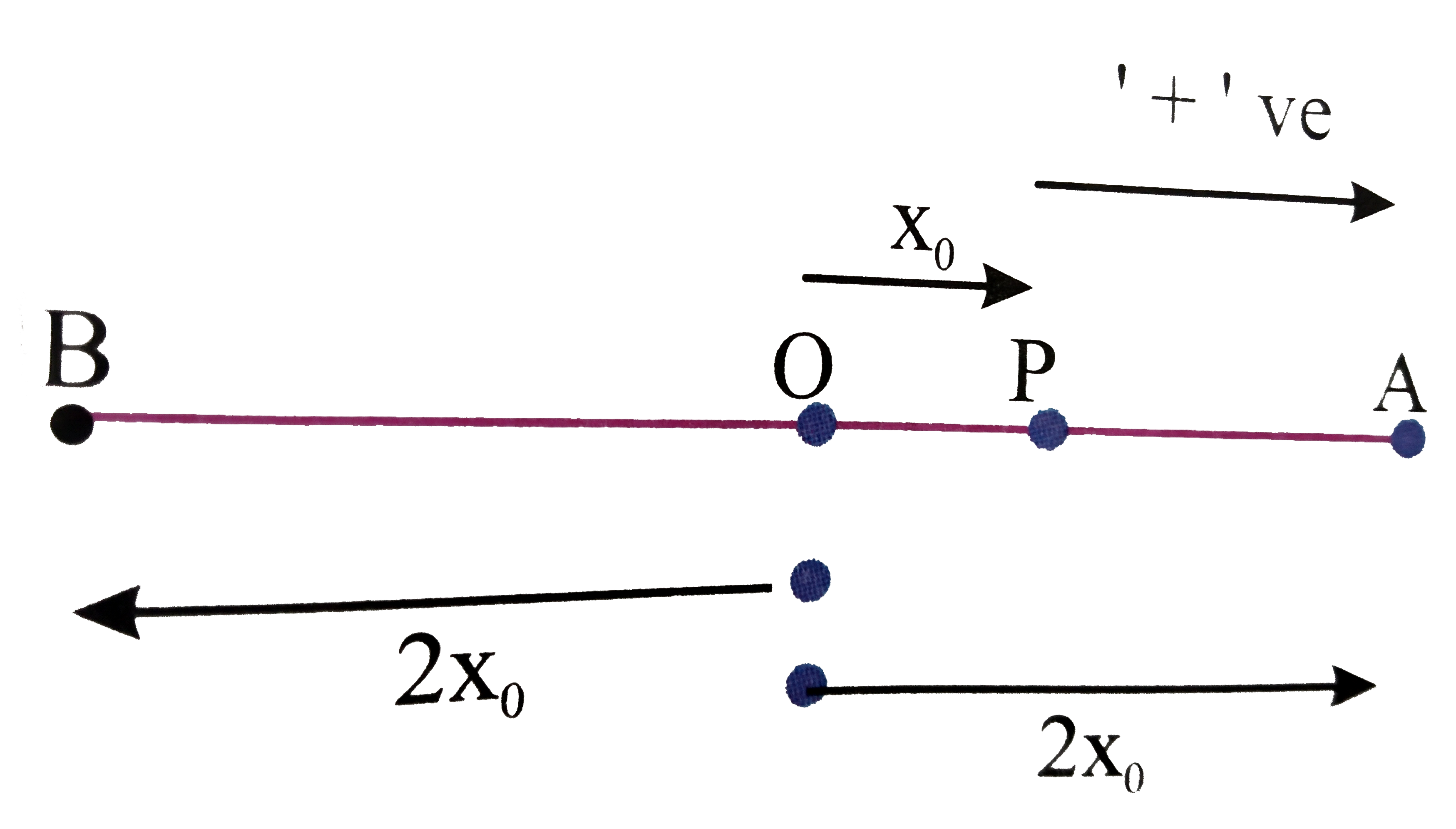
But in the given situation velocity of block at `P` will get....with same magnitude, mass `PA` part of motion will be......Equation of motion `x =- 2x_(0) cos omegat` for `t_(BP) , x = x_(0) rArr x_(0) =- 2x_(0) cos omegat_(BP)`
`rArr omegat_(BP) = ((pi)/(2)+(pi)/(6)) rArr t_(BP) = (4pi)/(6 omega), t_(PB) = t_(BP)`
Net time period `T = 2t_(BP) = (8pi)/(6 omega) = (4)/(3)pi sqrt((m)/(k))`