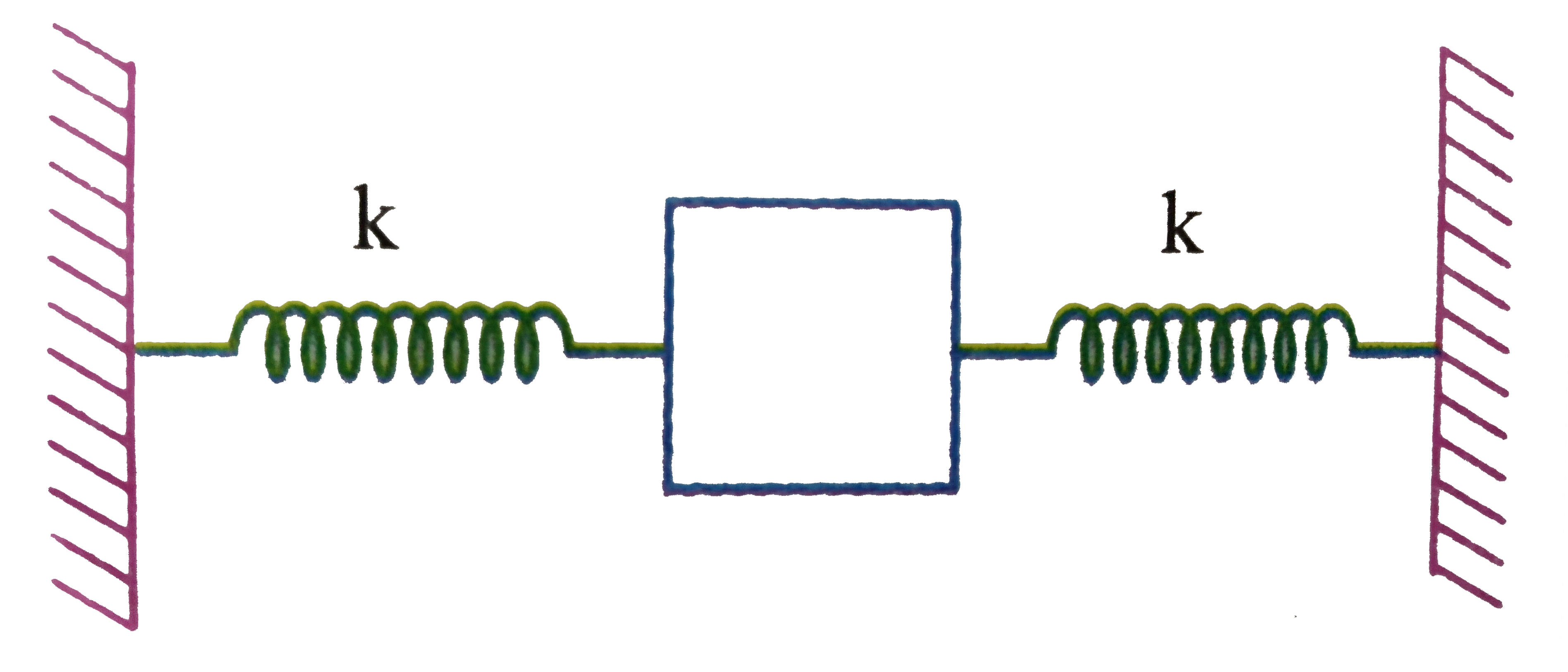
A block is tied within two springs, each having spring constant equal to `k`. Initially the springs are in their natural length and horizontal as shown. The block is released from rest. The springs are ideal, acceleration due to gravity is `g` downwards. air resistance is to be neglect. The natural length of spring is `l_(0)`.
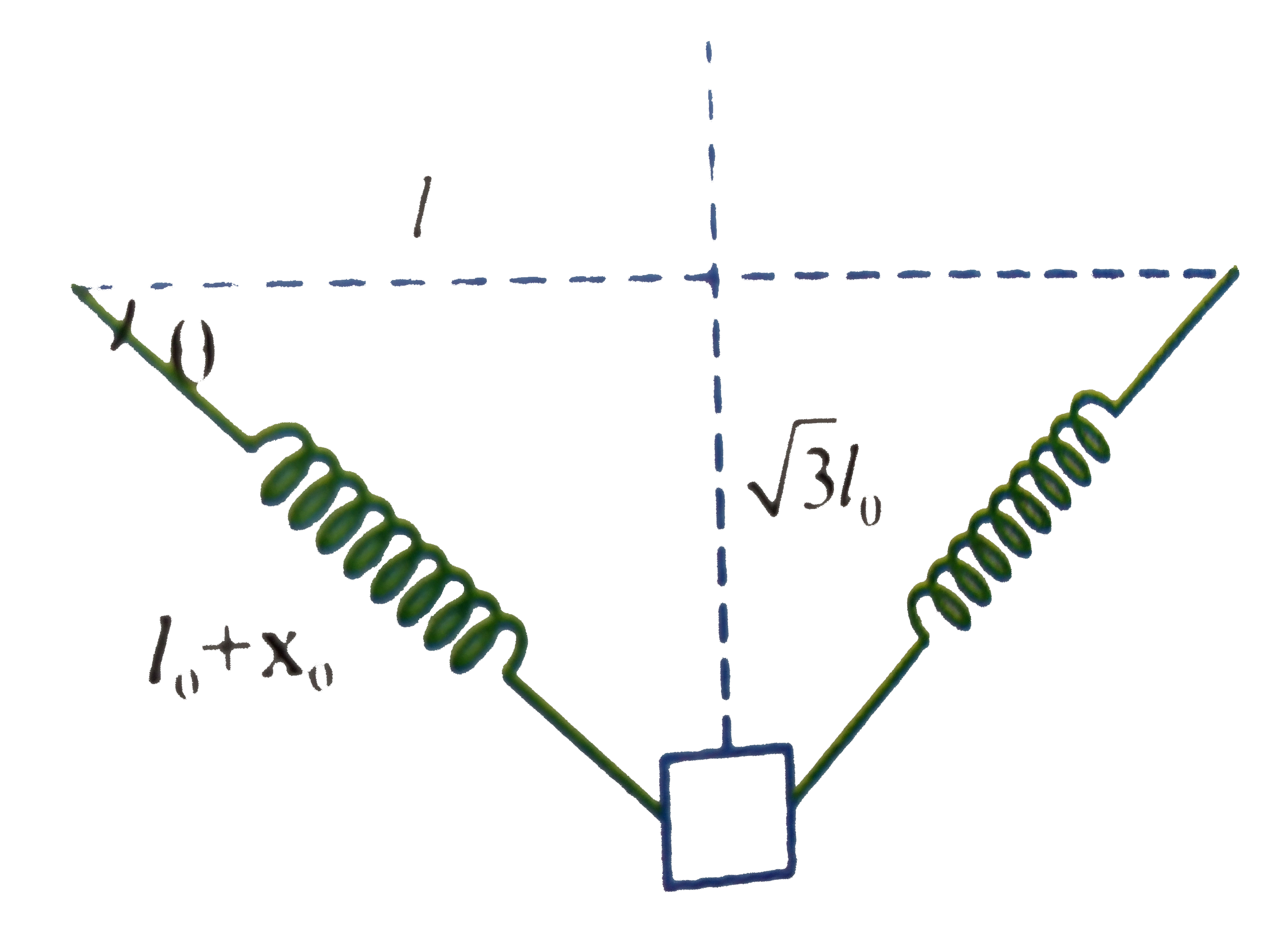
`l_(0) +x_(0) =sqrt(l_(0)^(2)+3l_(0)^(2)) = 2l_(0) rArr x_(0) = l_(0)`
`mg = [kx_(0) sin 60^(@)]2 = sqrt(3) kl_(0) rArr m = (sqrt(3)kl_(0))/(g)`
`tan theta = sqrt(3) rArr theta = 60^(@)`