A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
NARAYNA|Exercise Level-Vi Integer|9 VideosMOTION IN A PLANE
NARAYNA|Exercise Level-I (H.W)|41 VideosMOTION IN A PLANE
NARAYNA|Exercise Level-Vi multiple answer|16 VideosMECHANICAL PROPERTIES OF SOLIDS
NARAYNA|Exercise LEVEL-II (H.W)|24 VideosMOTION IN A STRAIGHT LINE
NARAYNA|Exercise Level 2 H.W|29 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-MOTION IN A PLANE-Level-VI Passage answer
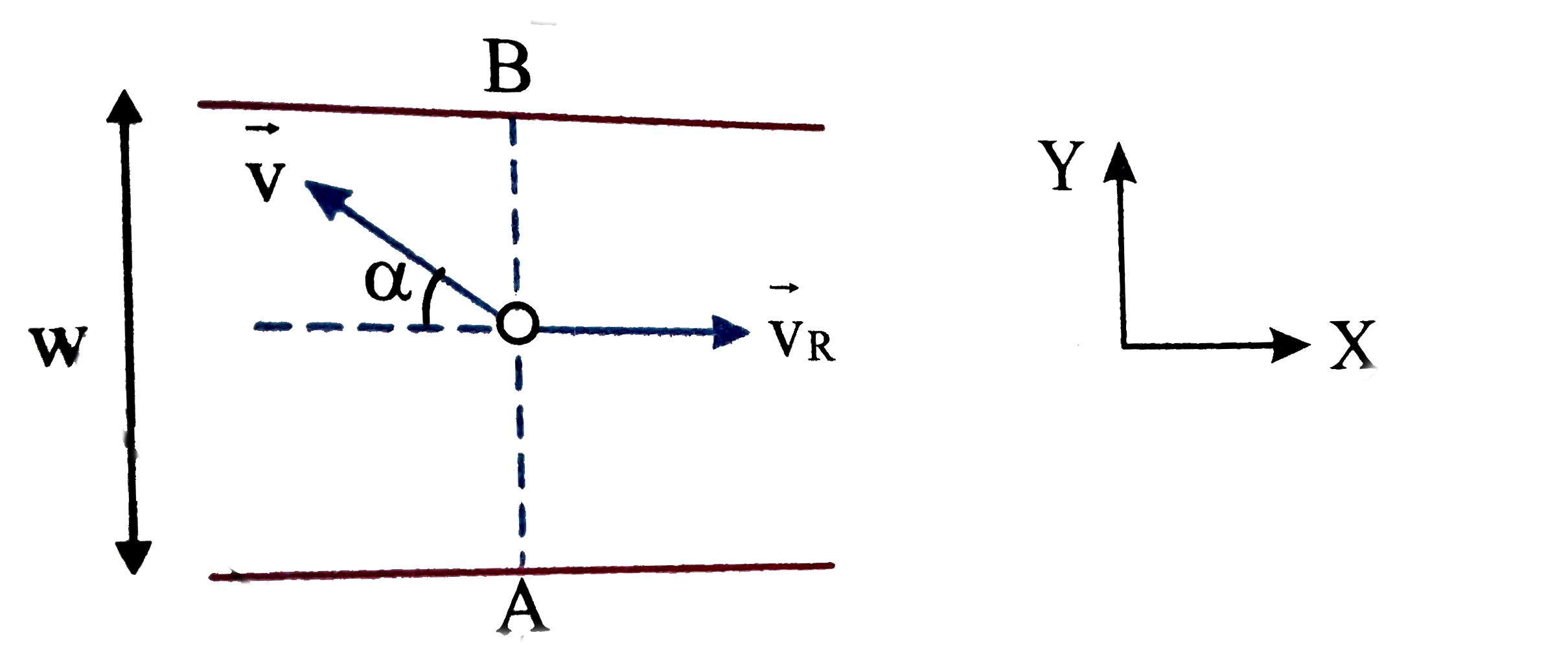
- A river of width w is flowing such that the stream velocity varies wit...
Text Solution
|
- A river of width w is flowing such that the stream velocity varies wit...
Text Solution
|
- A man is riding on a flat car travelling with a constant speed of 10m/...
Text Solution
|
- A man is riding on a flat car travelling with a constant speed of 10m/...
Text Solution
|
- A cannon is fixed with a smooth massive trolley car at an angle theta ...
Text Solution
|
- A cannon is fixed with a smooth massive trolley car at an angle theta ...
Text Solution
|
- A cannon is fixed with a smooth massive trolley car at an angle theta ...
Text Solution
|
- A cannon is fixed with a smooth massive trolley car at an angle theta ...
Text Solution
|
- When we analyse the projectile motion from any accelerated frame O as ...
Text Solution
|
- When we analyse the projectile motion from any accelerated frame O as ...
Text Solution
|
- A point moves in the plane xy according to the law, x=a sin omegat,y=a...
Text Solution
|
- A point moves in the plane xy according to the law, x=a sin omegat,y=a...
Text Solution
|
- A point moves in the plane xy according to the law, x=a sin omegat,y=a...
Text Solution
|
- At time t=0, the position vector of a particle moving in the x-y plane...
Text Solution
|
- At time t=0, the position vector of a particle moving in the x-y plane...
Text Solution
|
- The position vector of a particle at time t is given by vecr=2t hati+5...
Text Solution
|
- The position vector of a particle at time t is given by vecr=2t hati+5...
Text Solution
|
- The position vector of a particle at time t is given by vecr=2t hati+5...
Text Solution
|