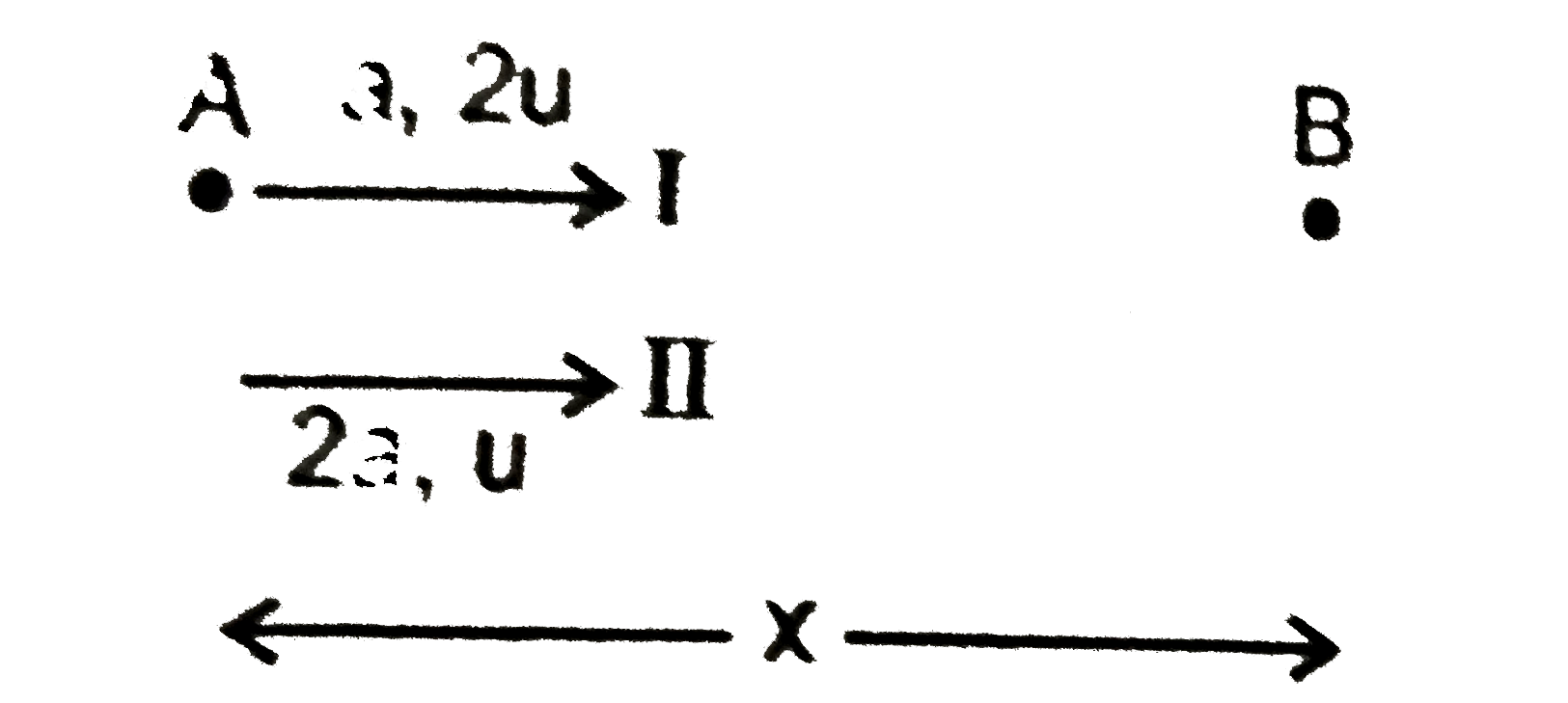Home
Class 11
PHYSICS
Two objects are moving along the same st...

Two objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time `t = 0.` The distance moved by the object when one overtakes the

A

`(6u^(2))/(a)`

B

`(2u^(2))/(a)`

C

`(4u^(2))/(a)`

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
A
Let both will meet at point `B`
`x=2ut+1/2at^(2)`
`x=ut+(1)/(2)(2a)t^(2)`
So `2ut+(1)/(2)at^(2)=ut+at^(2)`
`ut=(1)/(2)at^(2)rArrt=(2u)/(a)`
So `x=2u((2u)/(a))+(1)/(2)a((2u)/(a))^(2)=(6u^(2))/(a)`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 40|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 41|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 38|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

Two objects moving along the same straight line are leaving point A with an acceleration a , 2 a and velocity 2 u, u respectively at time t = 0 . The distance moved by the object with respect to point A when one object overtakes the other is :

An object moving along a straight line with a constant speed is said to be in _____

Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.

At the start of a motion along a line the initial velocity is u and acceleration is at. The final velocity vafter time t, is

For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as v=u+at , (u = initial velocity) Draw the velocity-time graph of the particle in following situations. (i) Velocity is decresing with time (i.e., acceleration in negative) (ii) Initial velocity is negative but acceleration is positive

Show that area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in the interval.

Show that the area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in that interval.

Two objects move in the same direction in a straight line. One moves with a constant velocity V_(1) .The other starts at rest and has constant acceleration a. They collide when the second object has velocity 2V_(1). The distance between the two objects when the second one starts moving is :