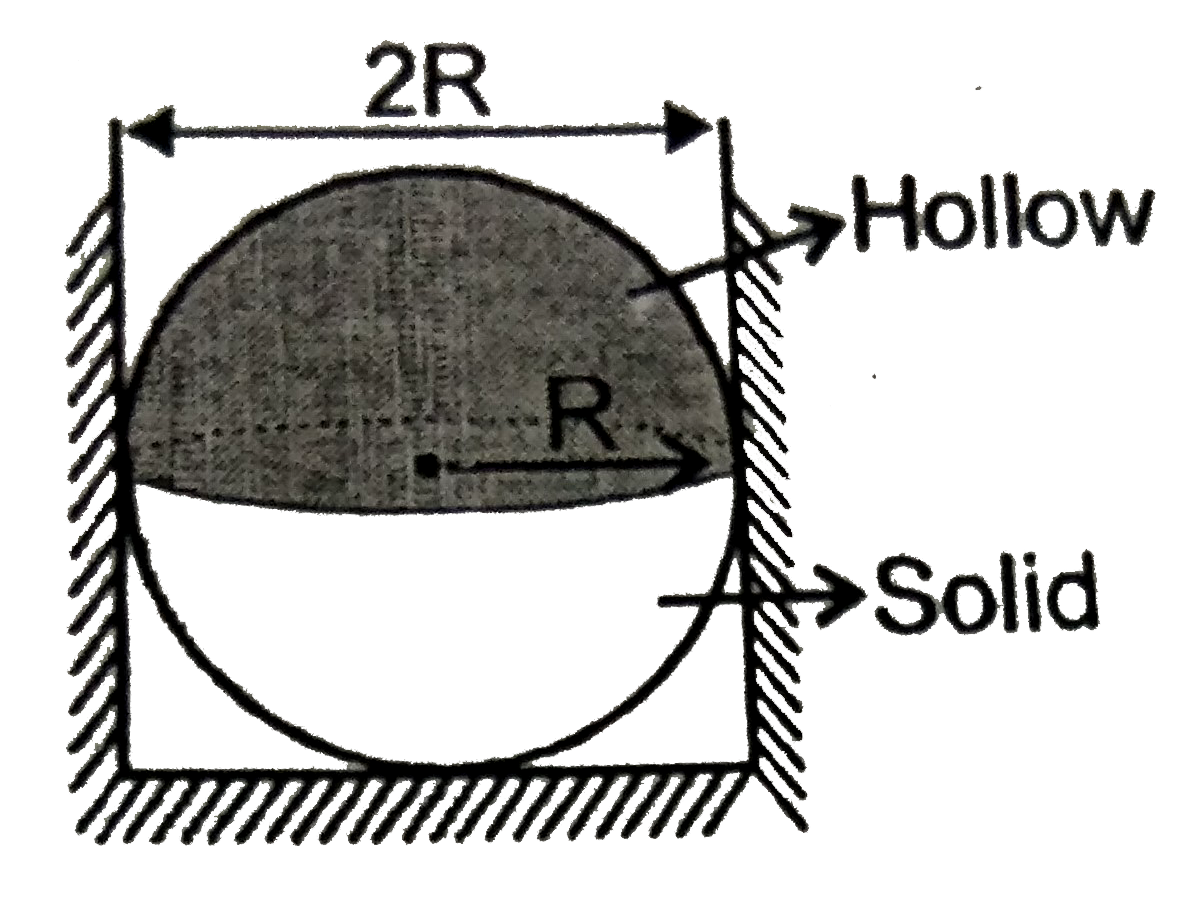
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP 65|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 66|4 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 63|5 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 64
- A compound sphere is made by joining a hemispherical shell and a solid...
Text Solution
|
- A particle is placed at the origin of the coordinate system. Two force...
Text Solution
|
- A railway compartments is 16 m long, 2.4 m wide and 3.2 m high. It is ...
Text Solution
|
- In the figure (i) a disc of mass M(kg) and radius R(m) is rotating smo...
Text Solution
|
- Block B of mass 2kg rests on block A of mass 10kg. All surfaces are ro...
Text Solution
|