A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.71|10 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.72|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.69|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.70
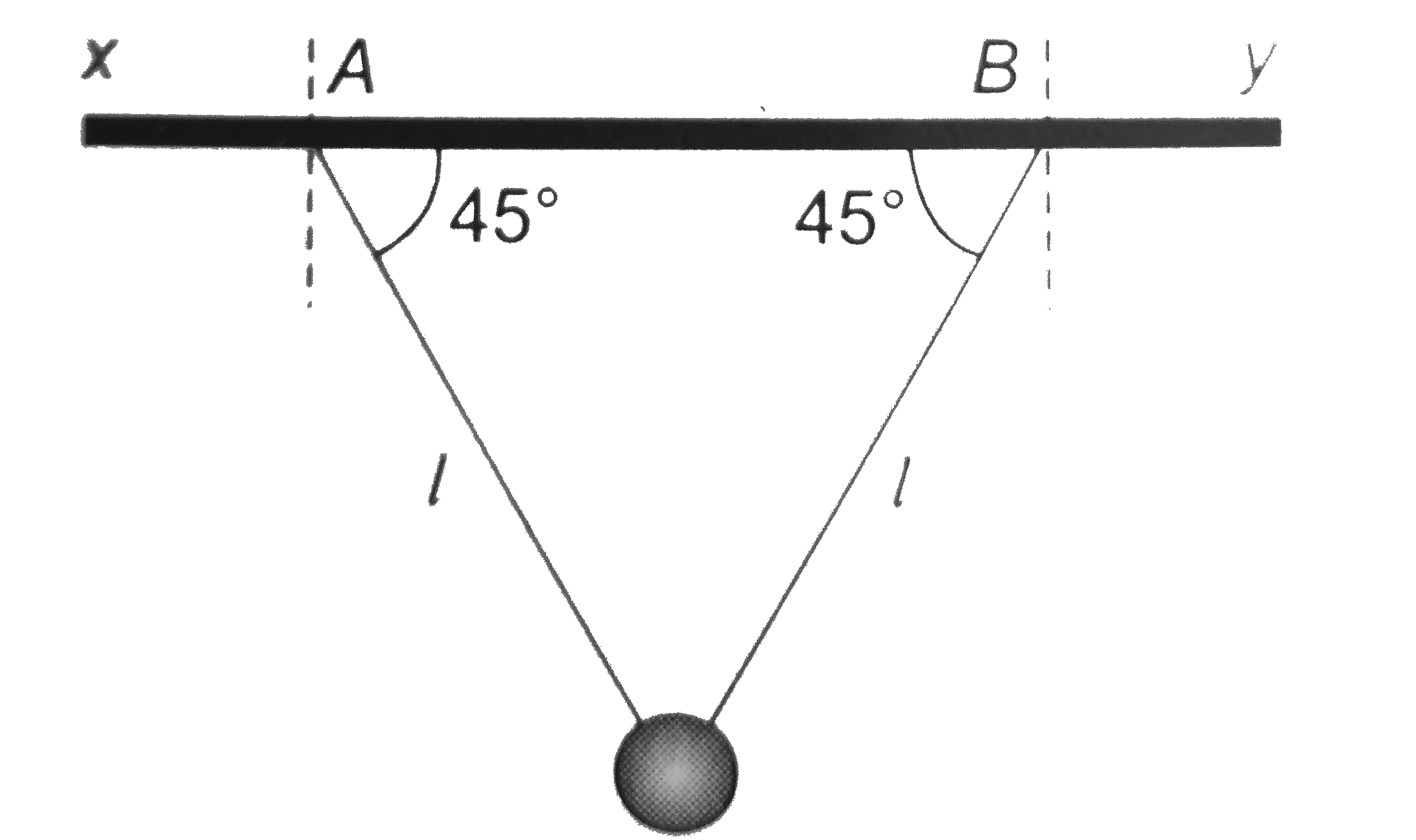
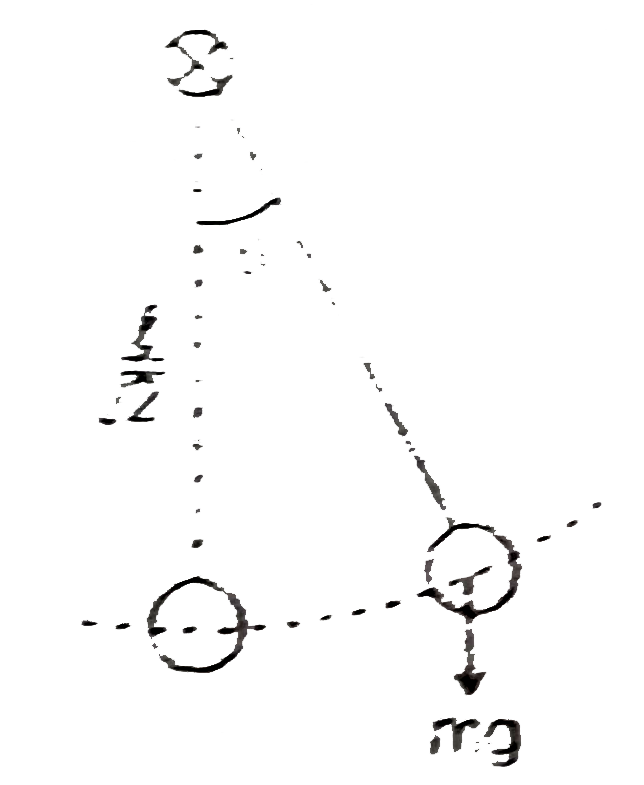
- Two light strings, each of length l are fixed at points A andB on a fi...
Text Solution
|
- A block A of mass 2 kg rests on a horizontal surface. Another block B ...
Text Solution
|
- A uniform disc of mass M and radius R is liffted using a string as sho...
Text Solution
|
- A ball is dropped on a large smooth inclined plane of angle of inclina...
Text Solution
|
- An electron is at P t = 0 It is circulating in anticlockwise direction...
Text Solution
|
- A heavy homogeneous cylinder has mass m and radius R. It is accelerate...
Text Solution
|
- An ideal gas undergoes a cyclic process abcda which is shown by pressu...
Text Solution
|
- A U-tube open from both ends, contain two arms, arm-1 and arm-2 each o...
Text Solution
|
- A U-tube open from both ends, contain two arms, arm-1 and arm-2 each o...
Text Solution
|