Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-ELECTROMAGNETIC INDUCTION AND AC CURRENT-Example
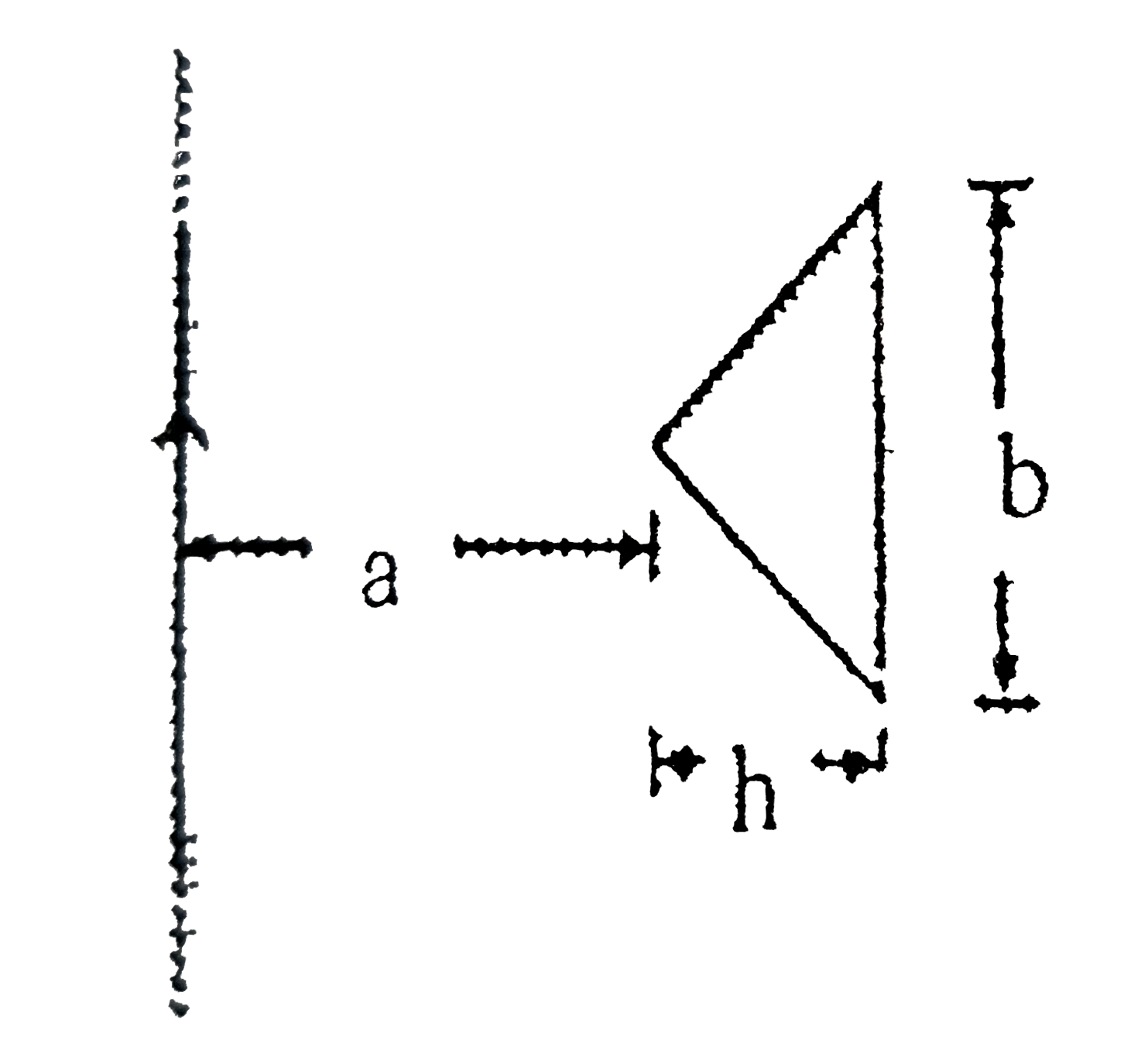
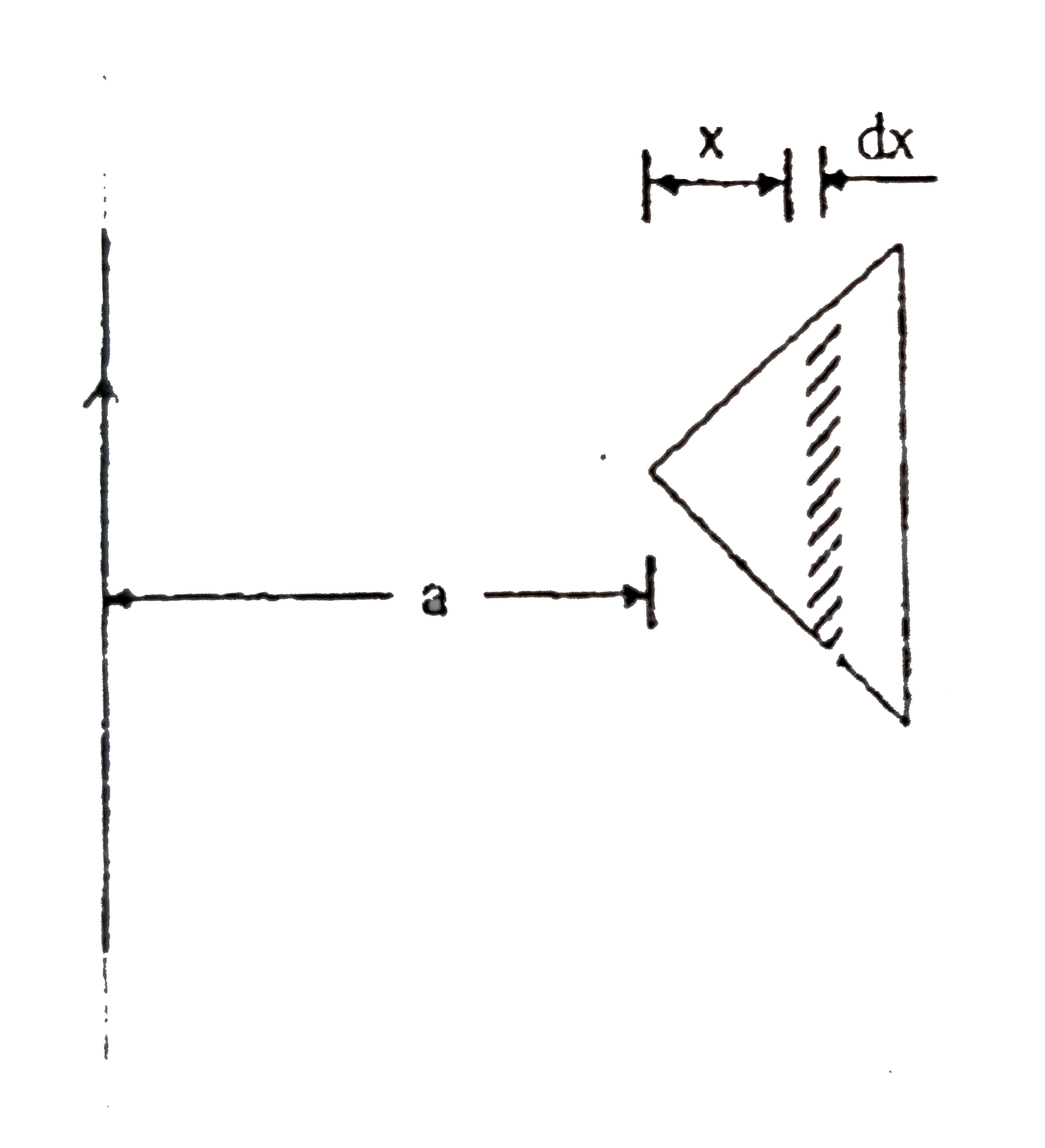
- A very long staright conductor and an isoceles triangular conductor li...
Text Solution
|
- A square loop of side 'a' with a capacitor of capacitance C is located...
Text Solution
|
- A conducting rod is bent as a parabola y=Kx^(2), where K is a constan...
Text Solution
|
- An iron core solenoid of length l and cross-sectional area A having N ...
Text Solution
|
- Two inductors of self inductances L(1) and L(2) of reistances R(1) and...
Text Solution
|
- shown in the figure is a small loop that is kept co-axially with the b...
Text Solution
|
- A conducting loop is pulled with a constant velocity towards a region ...
Text Solution
|
- A conducting bar is pulled with a constant speed v on a smooth conduct...
Text Solution
|
- A loop is kept so that its center lies at the origin of the coordinate...
Text Solution
|
- Shown in the figure is an R-L circuit. Just after the key (K) is close...
Text Solution
|
- A conducting loop of resistance R and radius r has its center at the o...
Text Solution
|
- The coefficient of mutual inductance of the two coils is 0.5 H. If the...
Text Solution
|
- An ideal choke takes a current of 8A when connected to an a.c. source ...
Text Solution
|
- A resistor R, an inductor L and a capacitor C are connected in series ...
Text Solution
|
- An AC source of angular frequency omega is fed across a resistor R and...
Text Solution
|