A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
UNIT DIMENSION, VECTOR & BASIC MATHS
BANSAL|Exercise EXERCISE - 2 [MATRIX TYPE]|1 VideosUNIT DIMENSION, VECTOR & BASIC MATHS
BANSAL|Exercise EXERCISE - 3 (Miscellaneous Exercise)|20 VideosUNIT DIMENSION, VECTOR & BASIC MATHS
BANSAL|Exercise EXERCISE - 1 [SINGLE CORRECT CHOICE TYPE]|34 VideosKINETIC THEORY OF GASES
BANSAL|Exercise Section-B|13 Videos
Similar Questions
Explore conceptually related problems
BANSAL-UNIT DIMENSION, VECTOR & BASIC MATHS-EXERCISE - 2 [MULTIPLE CORRECT CHOICE TYPE]
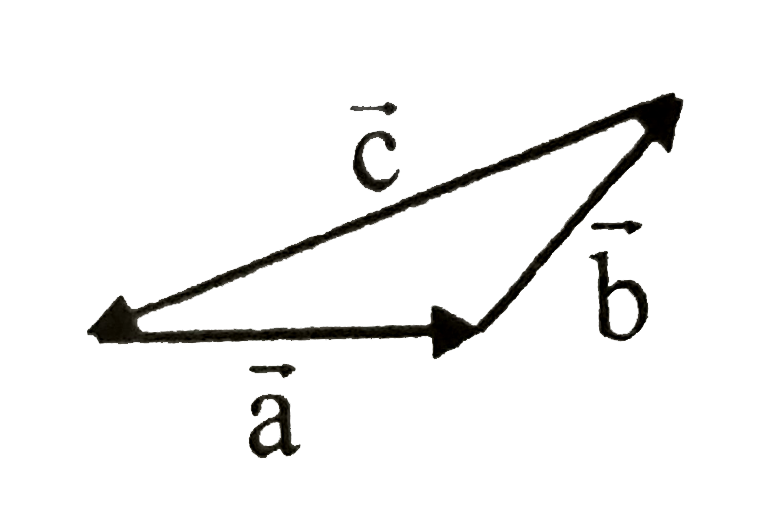
- Mark correct statement(s) for vec(a) , vec(b) and vec(c) shown in abo...
Text Solution
|
- Choose the correct statement. Assume ABCDEF to be a regular hexagon.
Text Solution
|
- Which of the following experssions has magnitude unity.
Text Solution
|
- A boy is pulling a block by a force of 10 N at an angle of 37^(@) to t...
Text Solution
|
- Vector vec(A)=(3hat(i)+4hat(j)-5hat(k)) is given find out the correct ...
Text Solution
|
- A man is standing at point (x=5m, y=0) . Then be walks along staight l...
Text Solution
|