Home
Class 12
PHYSICS
A uniform surface charge of density sigm...

A uniform surface charge of density `sigma` is given to a quarter of a disc extending up to infinity in the first quadrant of `x-y` plane. The centre of the disc is at the origin `O`. Find the z-component of the electric field at the point `(0,0,z)` and the potential difference between the point `(0,0,d)` and `(0,0,2d)`

Text Solution

Verified by Experts

The correct Answer is:
`(sigma)/(8 epsilon_(0))`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ELECTRIC POTENTIAL

    CENGAGE PHYSICS|Exercise DPP 3.3|20 Videos

  • ELECTRIC POTENTIAL

    CENGAGE PHYSICS|Exercise DPP 3.4|15 Videos

  • ELECTRIC POTENTIAL

    CENGAGE PHYSICS|Exercise DPP 3.1|14 Videos

  • ELECTRIC FLUX AND GAUSS LAW

    CENGAGE PHYSICS|Exercise MCQ s|38 Videos

  • ELECTRICAL MEASURING INSTRUMENTS

    CENGAGE PHYSICS|Exercise M.C.Q|2 Videos

Similar Questions

Explore conceptually related problems

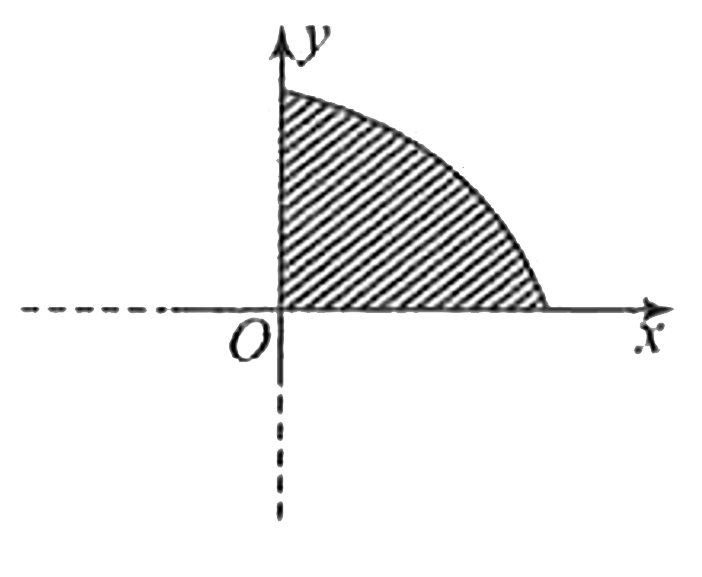
A uniform surface charge of density sigma is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0, 0, z) and the potential difference between the points (0, 0, d) & (0, 0, 2d) .

A unifrom surcace charfge of denstity sigma is given to quarter infinite non conducting place in fist quardrant of x-y plane . Find the z-compounct of the elctric field at the point (0, 0, x) Hence or otherwise find the potential difference between the points (0, 0, d) and (0, 0, 2d) .

Knowledge Check

  • The surface charge density of a thin charged disc of radius R is sigma . The value of the electric field at the centre of the disc is (sigma)/(2epsi_0) . With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc

    A
    reduces by 70.7%
    B
    reduces by 29.3%
    C
    reduces by 9.7%
    D
    reduces by 14.6%

  • A circular ring of radius R and uniform linear charge density +lamdaC//m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R/sqrt(2)) is

    A
    `lamda/(3sqrt(3)epsilon_0R)`
    B
    `(2lamda)/(3sqrt(3)epsilon_0R^2)`
    C
    `2/(3sqrt(3))lamda/(epsilon_0R)`
    D
    none the these

  • The electric potential at any point x,y an z in metres is given by V = 3x^(2) . The electric field at a point (2,0,1) is

    A
    `12 " Vm"^(-1)`
    B
    `-6 " Vm"^(-1)`
    C
    `6 " Vm"^(-1)`
    D
    `-12 " Vm"^(-1)`

    • Similar Questions

    Explore conceptually related problems

    A uniform electric field exists in x y plane as shown in Fig. 3.45. Find the potential difference. Between origin O and A(d,d,0) . .

    A circular ring lying in the x-y plane with its centre at the origin carries a uniformly distributed positive charge. The variation of the electric field E at the point (0,0,z) is correctly represented by the graph is

    The quarter disc of radius R (see figure) has a uniform surface charge density sigma . (a) Find electric potential at a point (O,O,Z) (b). Find the Z component of electrif field at (O,O,Z)

    A circular coil with 100 turns and radius 20 cm is kept in Y-Z plane with its centre at the origin. Find the magnetic field at point (20 cm, 0, 0) if coil carries a current of 2.0 A.

    The electric potential at a point (x, y, z) is given by V=-xy+z-z^3yx . The electric field vecE at the point (1,0,1) is (all quantities are in SI units)

    Home
    Profile