A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
NEWTONS LAWS OF MOTION
PHYSICS GALAXY - ASHISH ARORA|Exercise Numerical MCQs|90 VideosNEWTONS LAWS OF MOTION
PHYSICS GALAXY - ASHISH ARORA|Exercise Advance MCQs|17 VideosNEWTONS LAWS OF MOTION
PHYSICS GALAXY - ASHISH ARORA|Exercise Discussion Question|39 VideosLINEAR MOMENTUM & ITS CONSERVATION
PHYSICS GALAXY - ASHISH ARORA|Exercise exercise 1.3|3 VideosRIGID BODIES AND ROTATIONAL MOTION
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numerical|63 Videos
Similar Questions
Explore conceptually related problems
PHYSICS GALAXY - ASHISH ARORA-NEWTONS LAWS OF MOTION-Conceptual MCQs
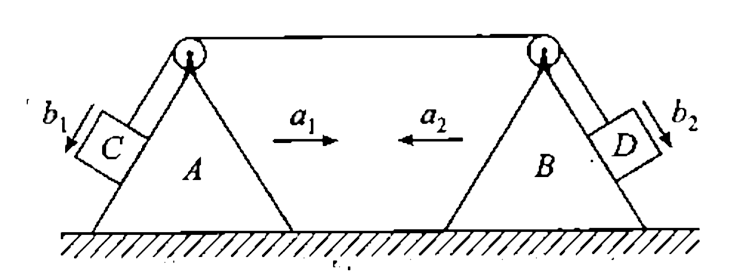
- Let a(1) & a(2) are the acceleration of A & B. Let b(1) & b(2) the acc...
Text Solution
|
- While walking on ice, one should take small steps to avoid sliping. Th...
Text Solution
|
- In the arrangement shown in figure-2.124 pulley A and B are massless a...
Text Solution
|
- A ball is dropped vertically from a height d above the ground . It hit...
Text Solution
|
- A bicycle moves on a horizontal road with some acceleration. The force...
Text Solution
|
- Consider the situation shown in figure. The wall is smooth but the sur...
Text Solution
|
- A block is about to slide down an inclined plane when its inclination ...
Text Solution
|
- Two objects A and B are thrown upward simultaneously with the same spe...
Text Solution
|
- Block A is placed on block B, whose mass is greater than that of A. Th...
Text Solution
|
- A body of mass M is applying horizontal force to slide a box of mass M...
Text Solution
|
- A block rests on a rough plane whose inclination theta to the horizont...
Text Solution
|
- In the balance machine, shown in the figure-2.127 which arm will move ...
Text Solution
|
- In a situation the contact force by a rough horizontal surface on a bo...
Text Solution
|
- In the figure the block A,B and C of mass m each, have acceleration a(...
Text Solution
|
- A block kept on an inclined surface, just begins to slide if the incli...
Text Solution
|
- When the force of constant magnitude always act perpendicular to the m...
Text Solution
|
- Essential characteristic of equilibrium is:
Text Solution
|
- The force required to stretch a spring varies with the distance a show...
Text Solution
|
- A person standing oin the floor of an elevator drops as coin. The coin...
Text Solution
|
- A scooter starting from rest moves wilth as constant acceleration for ...
Text Solution
|