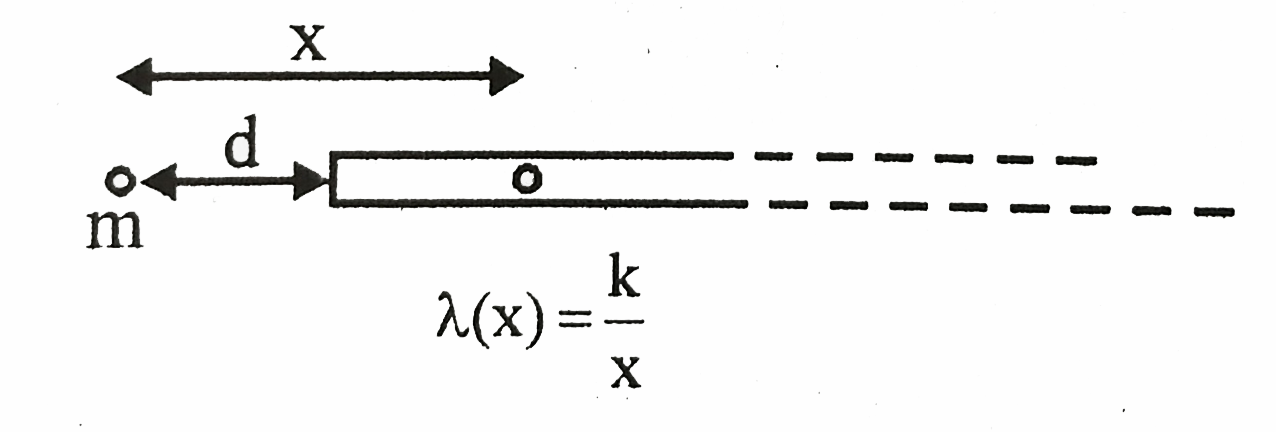Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
MOTION|Exercise Exercise - 4 | Level - I (Previous year | JEE Main)|16 VideosGRAVITATION
MOTION|Exercise Exercise - 4 | Level - II (Previous Year | JEE Advanced)|15 VideosGRAVITATION
MOTION|Exercise Exercise - 3 | level - 1 (Subjective | JEE Advanced)|13 VideosGEOMETRICAL OPTICS
MOTION|Exercise Exercise - 4 | Level-II|55 VideosHEAT - 1
MOTION|Exercise EXERCISE -4 (Level - II) Previous Year | JEE Advanced|22 Videos
Similar Questions
Explore conceptually related problems
MOTION-GRAVITATION-Exercise - 3 | Level - II (Subjective | JEE Advanced)
- Find the gravitational force of interaction between the mass m and an ...
Text Solution
|
- Calculate the ratio of the mean densities of the earth and the sun fro...
Text Solution
|
- Find the gravitational force between a point like mass M and an infini...
Text Solution
|
- A ring of radius R is made from a thin wire of radius r. If rho is the...
Text Solution
|
- A satellite P is revolving around the earth at a height h=radius of ea...
Text Solution
|
- A certain triple-star system consists of two stars, each of mass m, re...
Text Solution
|
- A man can jump over b=4m wide trench on earth. If mean density of an i...
Text Solution
|
- A launching pad with a spaceship is moving along a circular orbit of t...
Text Solution
|
- A satellite of mass m is in an elliptical orbit around the earth of ma...
Text Solution
|
- Assume that a tunnel is dug across the earth (radius=R) passing throug...
Text Solution
|