Home
Class 9
MATHS
ABCD is a parallelogram. A circle throug...

ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.

Text Solution

Verified by Experts

Given ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawm that it intersect AD at P and BC at Q
To prove Points P, Q, C and D are con-cyclic.

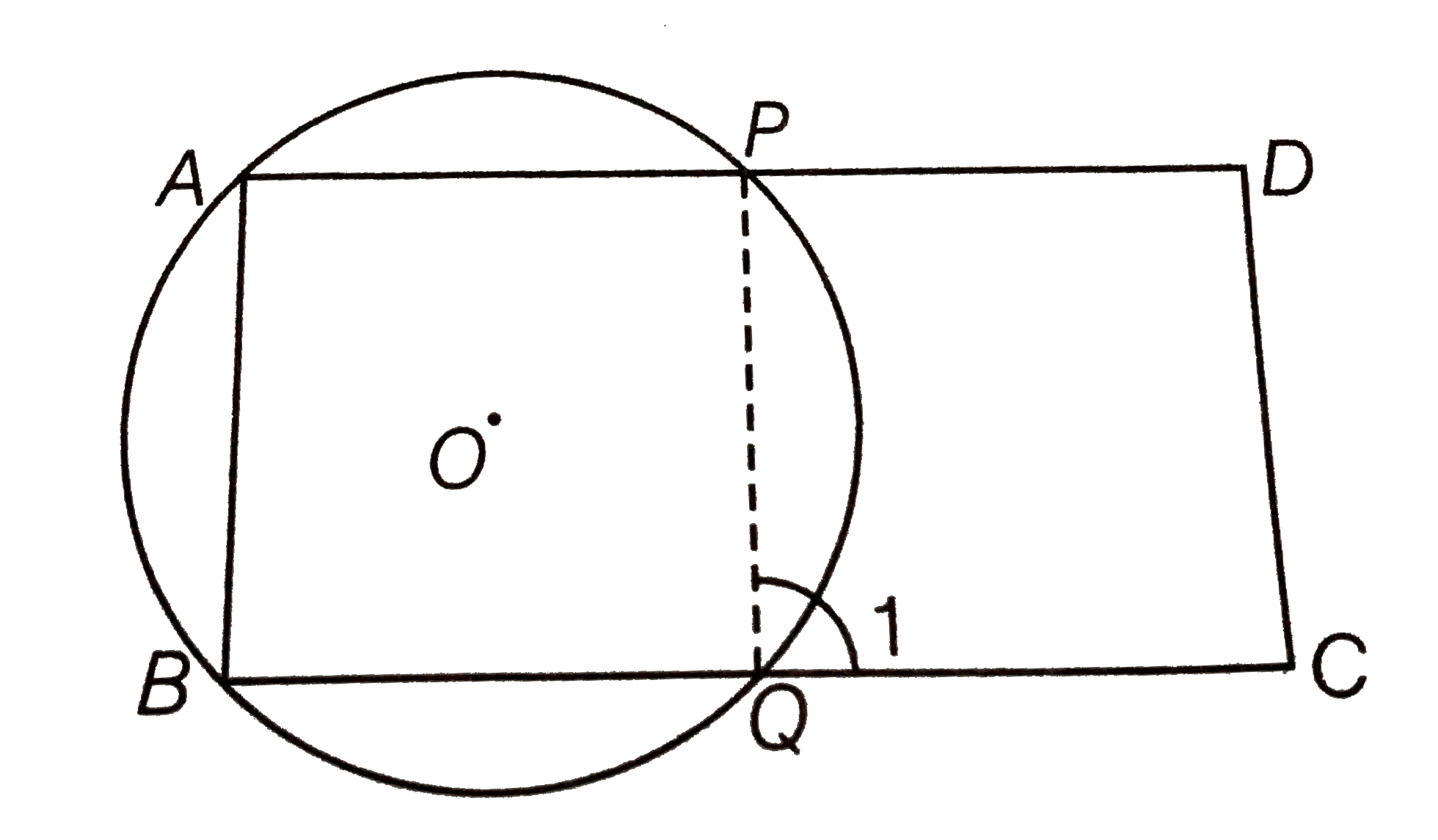
Construction Join PQ
Proof `angle1=angleA` [exterior angle property of cyclic quadrilateral]
But` angleA=angleC` [opposite angles of a parallelogram]
`:. angle1=angleC` ...(i)
But `angleC=angleD=180^(@)`
[sum of cointerior angles on same side is `180^(@)`]
`rArr angle1+angleD=180^(@)` [from Eq. (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q ,C and D are con-cyclic.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CIRCLES

    NCERT EXEMPLAR|Exercise Exercise 10.4|2 Videos

  • Areas of Parallelograms and Triangles

    NCERT EXEMPLAR|Exercise Areas Of Parallelograms And Triangles|34 Videos

  • CONSTRUCTIONS

    NCERT EXEMPLAR|Exercise Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

ABCD is a parallelogram.The circle through A ,B and C intersect CD( produced if necessary) at E.Prove that AE=AD

ABCD is a parallelogram.The circle through A,B and C intersects CD produced at E, prove that AE=AD

ABCD is a parallelogram.The circle through A.B and intersects CD produced at E.show that AD=AE .

The diagonals of a parallelogram ABCD intersect at a point O. Through O, a time is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.

The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.

P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.

The diagonals of a parallelogram A B C D intersect at a point Odot Through O , a line is drawn to intersect A D\ at P and B C at Qdot Show that P Q divides the parallelogram into two parts of equal area.

ABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD .

ABCD is a parallelogram. Any line through A cuts DC at a point P and BC produced at Q.Then,

ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar (Delta POA) =" ar "(Delta QOC) .

Home
Profile