Consider a horizontal parcel of air with cross-section A and height dh.
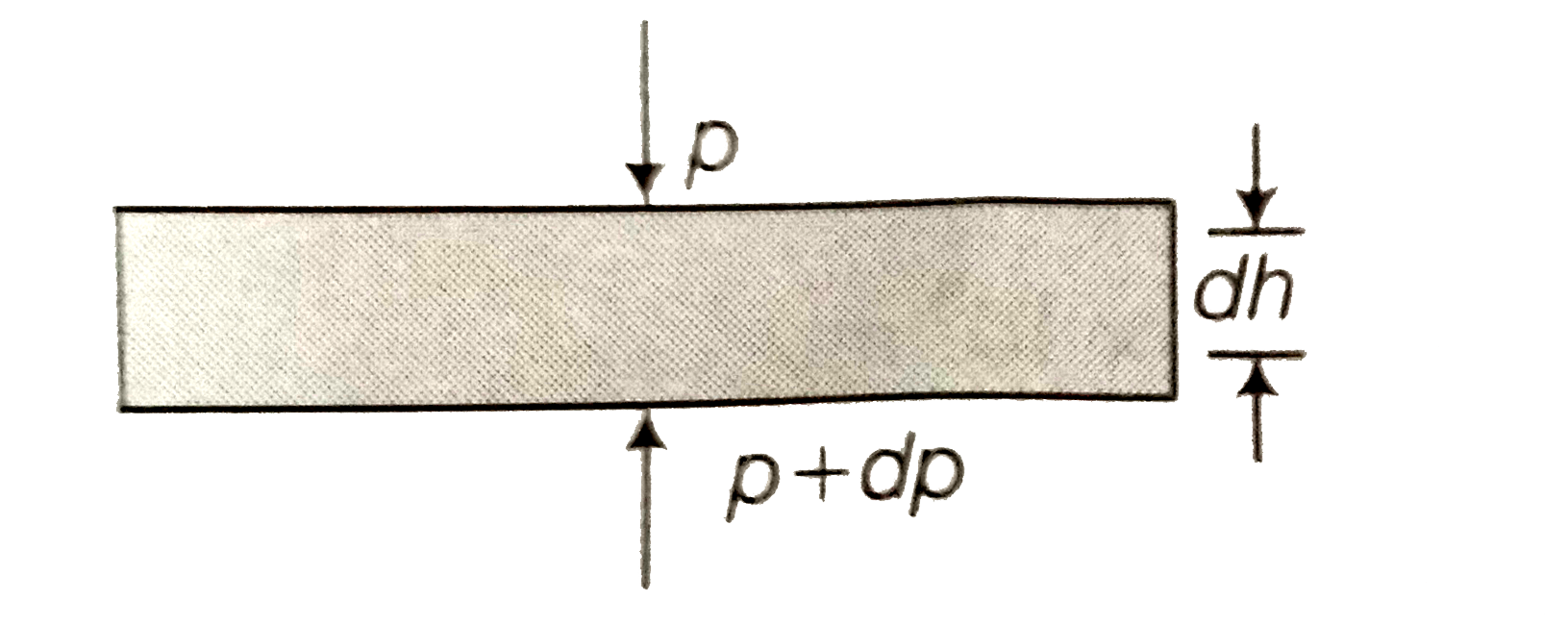
Let the pressure on the top surface and bottom surface be p and p+ dp. If the parcel is in equilibrium , then the net upward force must be balanced by the weight.
i.e., `(p+dp)A-pA=-rhogAdh" "(because` weight =Density `xx` Volume `xx g )`
`=-rhoxxAdh xx g`
`implies dp =-rhogdh. " "(rho=` density of air `)`
Negative sign shows that pressure decreases with height .
(b) Let `p_(@)` be the density of air on the surface of the earth.
As per question, pressure `prop` density
`implies (p)/(p_(@))=(rho)/(rho_(@))`
`implies rho=(rho_(@))/(p_(@))pdh" "[because dp=-rhogdh]`
`implies (dp)/(p)=-(rho_(@)g)/(p_(@))dh`
`implies underset(p_(@))overset(p)int (dp)/(p)=-(rho_(@)g)/(p_(@))underset(0)overset(h)int dh " "{:[(because "at h" =0, r=p_(@)),("and at h" =h,p=p)]:}`
`implies "In" (p)/(p_(@))=-(rho_(@)g)/(p_(@))h`
By removing log, `p=p_(@)e(-(rho_(@)gh)/(p_(@)))`
(c) As `p=p_(@)e^(-(rho_(@)gh)/(p_(@)))`,
`implies "In" (p)/(p_(@))=-(rho_(@)gh)/(P_(@))`
By question,
`p=(1)/(10)p_(@)`
`implies "In"(((1)/(10)p_(@))/(p_(@)))=-(rho_(@)g)/(p_(@))h`
`implies "In"(1)/(10)=-(rho_(@)g)/(p_(@))hrho_(@)`
`h=-(p_(@))/(rho_(@)g)"In"(1)/(10)=-(p_(@))/(p_(@)g)"In"(10)^(-1)=(p_(@))/(p_(@)g)"In"10`
`=(p_(@))/(rho_(@)g)xx2.303" "` [`because` In `(x)=2.303 "log"_(10)(x)]`
`=(1.013xx10^(5))/(1.22xx9.8)xx2.303=0.16xx10^(5)`m
`=16xx10^(3) `m
(d) We know that `" "p prop rho` (when T=constant i.e., isothermal pressure)
Temperature (T) remains constant only near the surface of the earth , not at greater heights.