Home
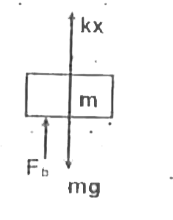
Class 12
PHYSICS
A cube of mass m and density D is suspen...

A cube of mass `m` and density `D` is suspended from a point `P` by a spring of stiffness `k`. The system is kept inside a beaker filled with a liquid of density `d`. The elongation in the spring, assuming `D gt d`, is :

A

`(mg)/k (1-d/D)`

B

`(mg)/1 (1-D/d)`

C

`(mg)/k (1+d/D)`

D

None of these

Text Solution

Verified by Experts

The cube is in equilibrium under the following three forces ,
spring force kx , where x = elongation of the spring ,
gravitional force w , weight of the cube = mg
buoyant force `F_(b)` ( or upward thrust ) imparted by the liquid on the cube given as `F_(b) = Vdg` where V = volume of the immersed portion of the cube equilibrium of the cube , ` kx + F_(b) = mg`
`rArr x = (mg -F_(b))/(k) = (mg- Vdg)/k ` where V = volume he immersed portion of the cube , For complete immersion , V = volume of the cube
For equilibrium of the cube , ` kx + F_(b) = mg`
` rArr = (mg-F_(b))/k = (mg-Vdg)/k ` Where V = (m/D)
` rArr x = (mg)/k (1- d/D)`
Hence (A) is correct
Promotional Banner

Topper's Solved these Questions

  • FLUID MECHANICS

    FIITJEE|Exercise LINKED COMPREHENSION TYPE|2 Videos

  • FLUID MECHANICS

    FIITJEE|Exercise LINKED COMPREHENSION TYPE I|1 Videos

  • FLUID MECHANICS

    FIITJEE|Exercise SOLVED PROBLEMS (SUBJECTIVE)|10 Videos

  • ELECTROSTATICS

    FIITJEE|Exercise Example|14 Videos

  • GENERAL PHYSICS

    FIITJEE|Exercise MATRIX MATCH TYPE|3 Videos

Similar Questions

Explore conceptually related problems

A cube of mass m and densituy D is suspended from the point P by a spring of stiffness k, The system is kept inside a beaker filled with a liquid of density d, where D gt d. What is the elongation in the spring ?

A sphere of density d is let fall in a liquid of density (d)/(4) . The acceleration of the body will be

A disc of mass m is connected with an ideal spring of stiffness k . If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:

A block of mass m suspended from a spring of spring constant k . Find the amplitude of S.H.M.

A body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:

A vessel filled with water is kept on a weighing pan and the scale adjusted of zero. A block of mass M and density rho is suspended by a masselss spring of spring constant k. This block is submerged inside into the water in the vessel. What is the reading of the scale /

A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

A vessel filled with water is kept on a weighing pan and the scale adjusted to zero. A block of mass 10 kg is suspended by a massless spring of spring constant k=100N//m . This block is submerged inside into the water in the vessel such that elongation i spring is x=10cm . What is the reading of the scale?

A mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring. The extension produced in the spring is given by

A block of mass m and relative density y( lt 1) si attached to an ideal spring of constant K. The system is initially at rest and at equilibrium. If the container acceleration upwards with a_(0) , find the increase in the elongation of the spring in equilibrium.

Knowledge Check

  • A sphere of density d is let fall in a liquid of density (d)/(4) . The acceleration of the body will be

    A
    `(g)/(4)`
    B
    `(3g)/(4)`
    C
    `(g)/(2)`
    D
    g

  • A disc of mass m is connected with an ideal spring of stiffness k . If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:

    A
    `(mg sin theta)/k`
    B
    `(2mg sin theta)/(3k)`
    C
    `(3mg sin theta)/k`
    D
    `(2 mg sin theta)/k`

  • A body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:

    A
    Vdg
    B
    `V rho g`
    C
    `V(rho -d)g`
    D
    `V(d-rho)g`