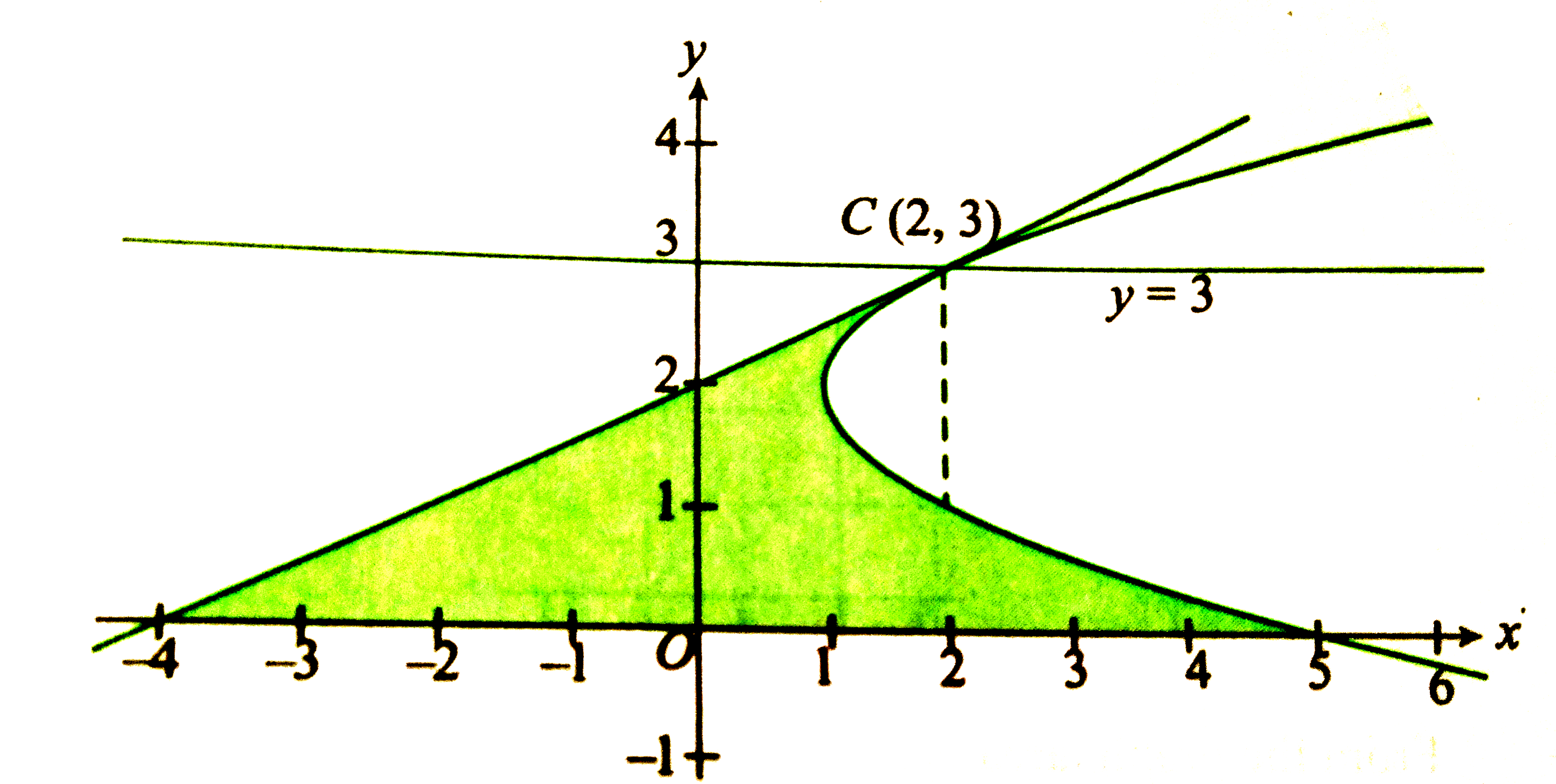
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-AREA-JEE Main Previous Year
- The area of the region bounded by the parabola (y""""2)^2=""x""""1 , t...
Text Solution
|
- The area bounded by the curves y=cosx and y=sinx between the ordinates...
Text Solution
|
- The area of the region enclosed by the curves y=x, x=e,y=(1)/(x) and t...
Text Solution
|
- The area bounded between the parabolas x^(2)=(y)/(4) and x^(2)=9y and ...
Text Solution
|
- The area (in square units) bounded by the curves y=sqrt(x),2y-x+3=0, x...
Text Solution
|
- The area of the region described by A = {(x,y) : x^2 + y^2 lt= 1and y^...
Text Solution
|
- The area (in sq. units) of the region described by {(x ,""y)"":""y^...
Text Solution
|
- The area (in sq units) of the region {(x, y) : y^2 gt= 2x and x^2 + y^...
Text Solution
|
- The area (in sq units) of the region bounded by the curve y = sqrtx an...
Text Solution
|
- Let g(x)=cos^2 x,f(x)=sqrtx and alpha,beta (alpha <beta) be the root...
Text Solution
|