Home
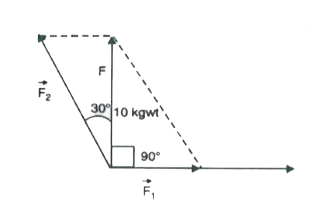
Class 12
PHYSICS
The resultant of two forces acting an an...

The resultant of two forces acting an angle of `120^(@)` is 10 kg wt and is perpendicular to one of the forces .That force is

A

`10sqrt(3)`kg wt

B

`20sqrt(3)` kg wt

C

10 kg wt

D

`10/sqrt(3)` kg wt

Text Solution

Verified by Experts

The correct Answer is:
D
Let two forces be `vec(F_(1))` and `vec(F_(2))` inclined at an angle `theta = 120°`. Since resultant force is 10 kg wt and perpendicular to `vec(F_(1))` . So `vec(F_(2))` makes angle with `vec(F)`

`:.F_(2)cos30^@=F`
`F_(2)10/(cos30^@)=(10xx2)/sqrt(3)=20/sqrt(3)kg wt`
Also `F_(2)sin30^@=F_(1)`
`:.F_(1)=20/sqrt(3)xx1/2=10/sqrt(3)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION

    MODERN PUBLICATION|Exercise Revision TEST|36 Videos

  • DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION

    MODERN PUBLICATION|Exercise MCQ(LEVEL-III)(Questions from AIEEE/ JEE Examinations)|6 Videos

  • DESCRIPTION OF MOTION IN ONE DIMENSION

    MODERN PUBLICATION|Exercise Revision Test|45 Videos

  • E.M. INDUCTION AND A.C. CURRENTS

    MODERN PUBLICATION|Exercise RECENT COMPETITIVE QUESTIONS|31 Videos

Similar Questions

Explore conceptually related problems

Define resultant force.

The sum of the magnitudes of two forces acting at a point is 16 N. The resultant of these forces is perpendicular to the smaller force has a magnitude of 8 N. If the smaller force is magnitude x, then the value of x is

Knowledge Check

  • The resultant of two forces, one double than the other in magnitude, is perpendicular to the smaller of the two forces. The angle between the two forces is :

    A
    `60^(@)`
    B
    `120^(@)`
    C
    `150^(@)`
    D
    `90^(@)`

  • The resultant of two forces, one double the other in magnitude, is perpendicular to the smaller of the two forces, the angle between the two forces is

    A
    `120^(@)`
    B
    `60^(@)`
    C
    `90^(@)`
    D
    `150^(@)`

  • The resultant of two forces is 20 N when one of force is 20 sqrt(3) N and angle between two forces is 30° then what is value of second force ?

    A
    10N
    B
    20N
    C
    `20sqrt(3)N`
    D
    `10sqrt(3)N`

    • Similar Questions

    Explore conceptually related problems

    If the resultant of two forces is equal in magnitude to one of the components and perpendicular to it direction, find the other components using the vector method.

    The magnetic force acting on a moving charge is

    The square of the resultant of two equal forces acting at a point is equal to three times their product. Find the angle between them.

    The resultant of two forces is 20/3 N. If one of the force is 20 N and makes an angle of 30° with the resultant, the other force has a mangitude:

    If resultant of two forces vec F and vec F is F. The angle between two forces is :

    Home
    Profile