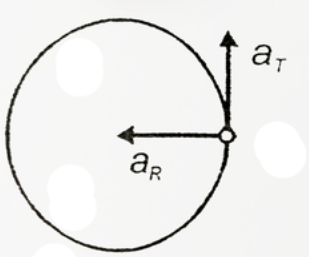
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
AAKASH INSTITUTE|Exercise Assignement section -E (Assertion-Reason)|3 VideosMOTION IN A PLANE
AAKASH INSTITUTE|Exercise Assignement section -G (Integer)|3 VideosMOTION IN A PLANE
AAKASH INSTITUTE|Exercise Assignement section -C Objective (More than one option is correct)|5 VideosMOCK_TEST_17
AAKASH INSTITUTE|Exercise Example|15 VideosMOTION IN A STRAIGHT LINE
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-MOTION IN A PLANE-Assignement section -D (Linked Comprehension)
- A particle moves with decreasing speed along the circle of radius R so...
Text Solution
|
- A particle moves with decreasing speed along the circle of radius R so...
Text Solution
|
- When a boat travels in a river (strictly in a straight line), it can g...
Text Solution
|
- When a boat travels in a river (strictly in a straight line), it can g...
Text Solution
|
- When a boat travels in a river (strictly in a straight line), it can g...
Text Solution
|
- Raindrops are falling with velocity 10 sqrt2 m/s making and angle 45^(...
Text Solution
|
- Raindrops are falling with velocity 10 sqrt2 m/s making and angle 45^(...
Text Solution
|
- Raindrops are falling with velocity 10 sqrt2 m/s making and angle 45^(...
Text Solution
|