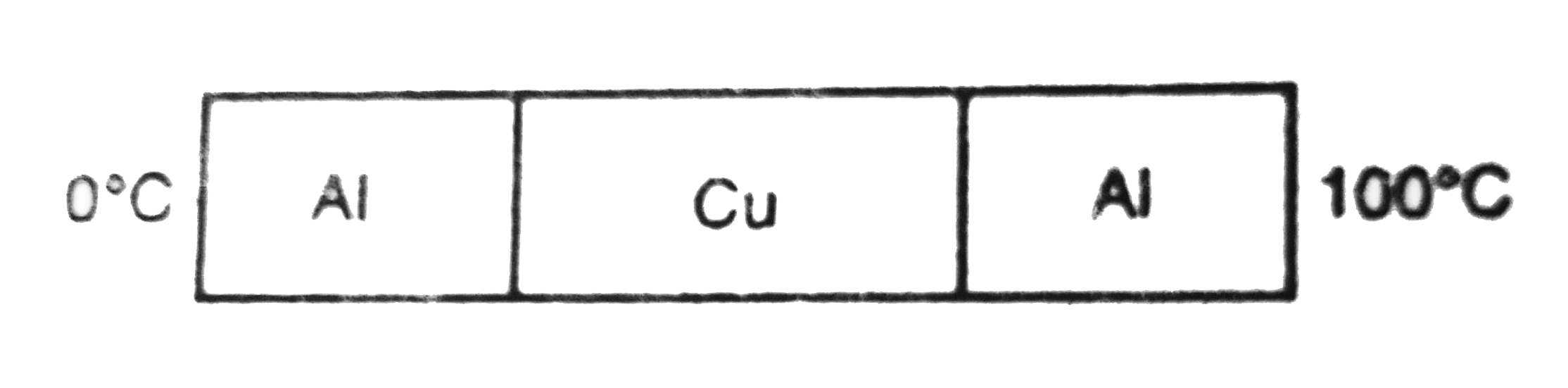
The three rods shown in figure have identical geometrical dimensions. Heat flows from the hot end at a rate of 40W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c). Thermal conductivities of aluminium and copper are `200Wm^(-1)`^(@)C^(-1)` and `00Wm^(-1)`^(@)C^(-1)` respectively.

Answer

D

Explanation

`theta_1=theta_2=100`
`(Q)/(T)=(Ka(theta_1-theta_2))/(t)`
`R=R_1+R_2+R_3` ltbrge =1/(ak_Al)+1/(ak_cu)+1/(ak_Al)`
`=1/a((2/200)+(1/400))`
`1/a((4+1)/400)=1/a 5/400`
`=1/a 1/80`
`Q/t=100/((1/a) (1/80))[:' Q/t=(theta_1-theta_2)/R]`
`40=80xx100xx(a/l)`
`[from question Q/t =40 W.]`
`a/l=1/200`
`for, B `R=R_1+R_2+R_3`
`=R_Al+(R_Cu R_Al)/R_Cu+R_Al)`
`=1/(aK_(Al))+((1)/(aK_(Cu)).(1)/(aK_(Al)))/((1)/(aK_(Cu)).(1)/(aK_(Al)))`
`=1/(aK_(Al))+(l)/(a(K_(al)+aK_(Cu))`
`=1/a((1)/(200)+(1)/(200+400))`
`=1/a((1)/(200)+(1)/(600))`
``=1/a((3+1)/(600))=(4/600).(l/a)`
`(Q/t)=(theta_1-theta_2)/R=(100)/((l/4) (4/600))`
`=(600xx100)/4xx(a/l)`
`=(300/4)=75[Using (a/l)=1/200)]`
`For C (1/R)=(1/R_1)+(1/R_1)+(1/R_1)`
`=(1//l)/(ak_(Al))+(1//l)/(ak_(Cu))+(1//l)/(ak_(Al))`
`=(K_(Al)+K_(Cu)+K_(Al)).(a/l)`
`=(2xx200xx400)(a/l)`
`=(a/l)(800)`
`implies R=(a/l)(1/800)`
`(Q/t)=(theta_1-theta_2)/R=(100)/((l/a)(1/800))`
`=(100xx800xxa)/l`
`=(100xx800)/200=400W.`