In the circuit shown in figure

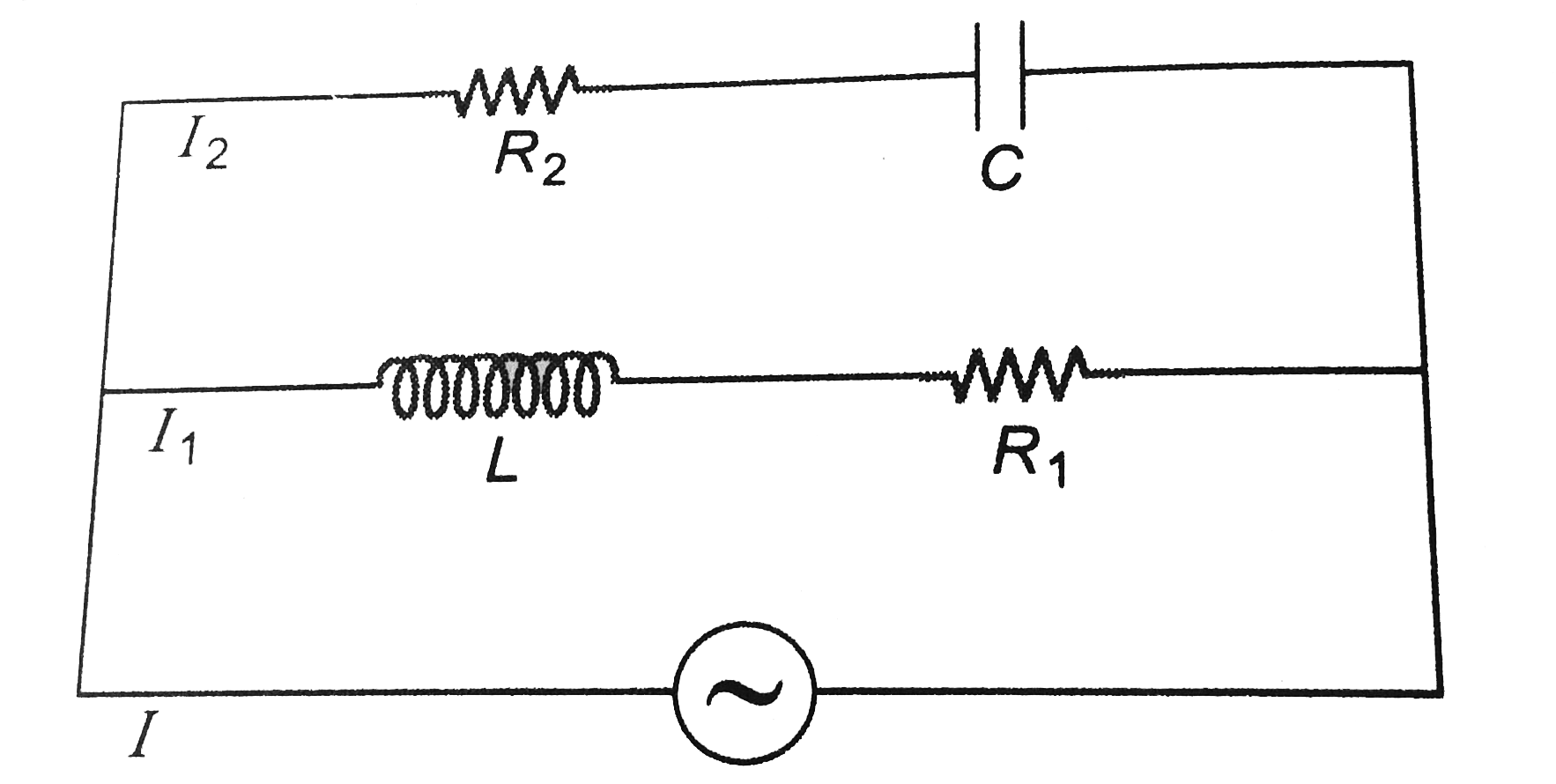
`R_1=30Omega, R_2=40 Omega, L=0.4H` and `C=1/3mF`.
Find seven function of time `I, I_1, I_2, V_(R_1), V_L, V_(R_2)` and `V_C`. Also total power consumed in the circuit. In the given potential function `V` is in volts and omega in `rad//s`.

Explanation

Circuit 1 (containing `L` and `R_1`)
`I_1: X_L=omegaL=100xx0.4=40Omega`
`R_1=30Omega`
`:. Z_1=sqrt(R_1^2+X_L^2)=sqrt((30)^2+(40)^2)`
`=50Omega` ltbRgt Maximum value of current `I_1=V_0/Z_1=200/50=4A`
Since there is only `X_L` so voltage function will lead the current function by angle `phi_1`, where
`cosphi_1=R_1/Z_1=30/50=3/5`
`:. phi_1=53^@`
`:. I_1=4sin(100t+30^(@)-53^(@))`
or `I_1=4sin(100t-23^@)`
`V_(R_1)-V_(R_1)` function is in phase with `I_1` function
Maximum value of `V_(B_1)`=(maximum value of `I_1`) `(R_1)`
`=(4)(30)`
`=120` volt
`V_(R_1)=120sin(100t-23^@)`
`V_L:V_L` function is `90^@` ahead of `I_1` function.
Maximum value of `V_L=` (maximum value of `I_1`) `(X_L)`
`=(4)(40)=160` volt
`V_L=160sin(100t-23^@+90^@)`
`:. V_L=160sin(100t+67^@)`
power in this circuit power will be consumed only across `R_1`. This power is given by
`P_(R_1)`=(rms value of `I_1)^2R_1`
`(4/sqrt2)^2(30)`
`=240watt`
Circuit 2 (containing `C` and `R_2`)
`I_2: X_C=1/(omega_C)=1/(100xx1/3xx10^-3)=30Omega`
`R_2=40 Omega`
`Z_2=sqrt(R_2^2+X_C^2)`
`=sqrt((40)^2+(30)^2)`
`=50 Omega`
Maximum value of `I_2=V_0/Z_2=200/50=4A`
Since, there is only `X_C,` so `I_2` function will lead the `V` function by an angle `phi_2` where
`cosphi_2=R_2/Z_2=40/50=4/5`
`:. phi_2=37^@`
`V_(R_1):V_(R_2) ` function is in phase with `I_2` function
Maximum value of `V_(R_2)=` (maximum value of `I_2`) `(R_2)`
`=4xx40=160` volt
`V_(R_2)=160sin(100t+67^@)`
`V_C:V_C` function lags `I_2` function of `90^@`
maximum value of `V_C=` (maximum value of `I_2`) `(X_C)`
`=4xx30`
`=120` volt
`V_C=120sin(100t+37^@-90^@)`
or `V_C=120sin(100t-23^@)`
Power in this circuit, power will be consumed only across `R_2` and this power is given by
`R_(R_2)` =(rms value of `I_2)^2R_2`
`=(4/sqrt2)^2(40)`
`=320W`
`:.` Total power consumed in the circuit
`P=P_(R_1)+P_(R_2)`
`(240+320)W`
`=560W`
`I: I=I_1+I_2`
`I=4sin(100t-23^@)+4sin(100t-67^@)`
Now the amplutide can be added by vector method.

Resultant of `4 A` and `4A` at `90^@` is `4sqrt2` at `45^@` from both currents or at `22^@` from 100 t line
`I=4sqrt2sin(100t+22^@)`.