Home
Class 11
PHYSICS
Three masses are atteched to strings rot...

Three masses are atteched to strings rotaing in the horizontal plank .The string pass over two naine as shown in fig will this system be in equilibrium

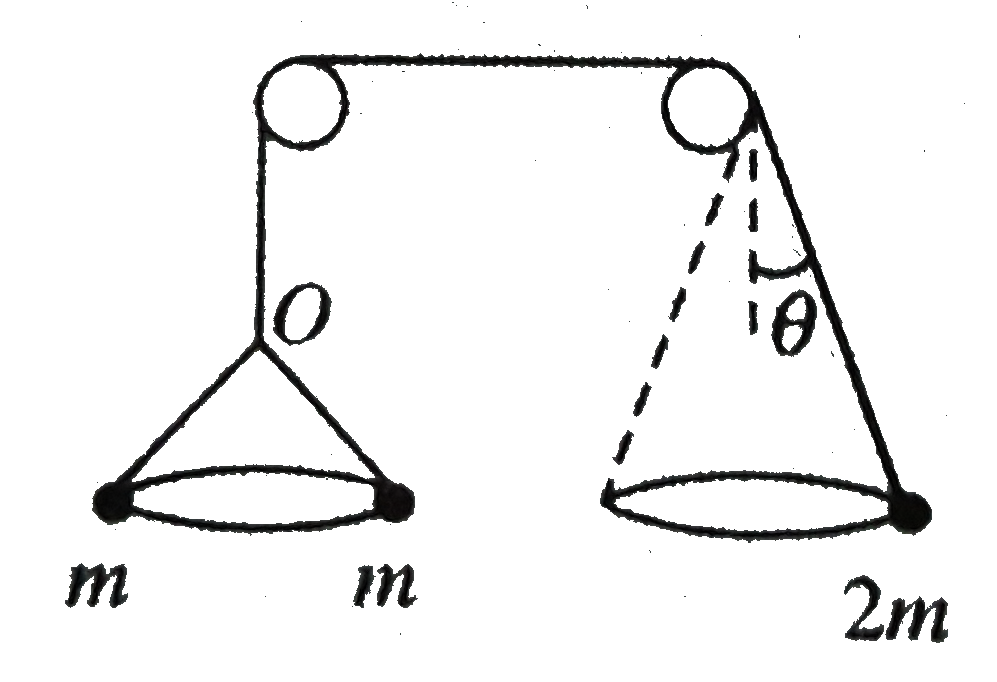
Text Solution

Verified by Experts

Considering the string over the left mail , the vertical components of the force of tension `T` acting on the weights are so the tension in the string above `O` is `T = 2 mg`
For the string on the right , the verticle component of the strings tension `T' is equal to `2 mg` (if the mass does not move down ) The tension of the along itself , however is `T = (2mg)/(cos theta) ge 2 mg` Therefore,the system is not in equalibrium .The right hand mass will have a greater pull.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • NEWTON'S LAWS OF MOTION 2

    CENGAGE PHYSICS|Exercise Subjective|21 Videos

  • NEWTON'S LAWS OF MOTION 2

    CENGAGE PHYSICS|Exercise Single Correct|87 Videos

  • NEWTON'S LAWS OF MOTION 2

    CENGAGE PHYSICS|Exercise Exercise 7.2|16 Videos

  • NEWTON'S LAWS OF MOTION 1

    CENGAGE PHYSICS|Exercise Integer|5 Videos

  • PROPERTIES OF SOLIDS AND FLUIDS

    CENGAGE PHYSICS|Exercise INTEGER_TYPE|2 Videos

Similar Questions

Explore conceptually related problems

Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then

Three loads of mass m_(1),m_(2) and M are suspended on a string passed through two pulleys as shown in Fig. The pulleys are at the same distance from the points of suspension. Find the ratio of masses of the loads at which the system is in equilibrium. Can these conditions always be realized? The friction should be neglected.

Knowledge Check

  • Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then

    A
    `tantheta=1+(2M)/(m)`
    B
    `tantheta=1+(2m)/(M)`
    C
    `cottheta=1+(2M)/(m)`
    D
    `cottheta=1+(2m)/(M)`

  • Two masses m and M are attached with strings as shown. For the system to be in equilibrium we have.

    A
    `tantheta=1+(2M)/(m)`
    B
    `tantheta=1+(2m)/(M)`
    C
    `tantheta=1+(M)/(2m)`
    D
    `tantheta=1+(m)/(2M)`

  • Three equal weights of mass 2 kg each are hanging on a string passing over a fixed pulley as shown in fig What is the tension in the string connecting weights B and C?

    A
    zero
    B
    13 N
    C
    `3.3 N`
    D
    `19.6 N`

    • Similar Questions

    Explore conceptually related problems

    Three identical masses are attached to the ends of light strings, the other ends of which are connected together as shown in the figure. Each of the three strings has a length of 3 m. The three masses are dropped through three holes in a table and the system is allowed to reach equilibrium. (a) What is total length of the strings lying on the table in equilibrium? (b) Select a point K inside the triangleABC such that AK + BK + CK is minimum, use the result obtained in (a) and the fact that potential energy of the system will be minimum when it is in equilibrium.

    Three equal weights of mass m each are hanging on a string passing over a fixed pulley as shown in fig. The tensions in the string connecting weights A to B and B to C will respectively be -

    A mass m moves in a circles on a smooth horizontal plane with velocity v_(0) at a radius R_(0) . The mass is atteched to string which passes through a smooth hole in the plane as shown. The tension in string is increased gradually and finally m moves in a cricle of radius (R_(0))/(2) . the final value of the kinetic energy is

    Two masses m and M(m lt M) are joined by a light string passing over a smooth and light pulley (as shown)

    The masses (M+m) and (M-m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .

    Home
    Profile