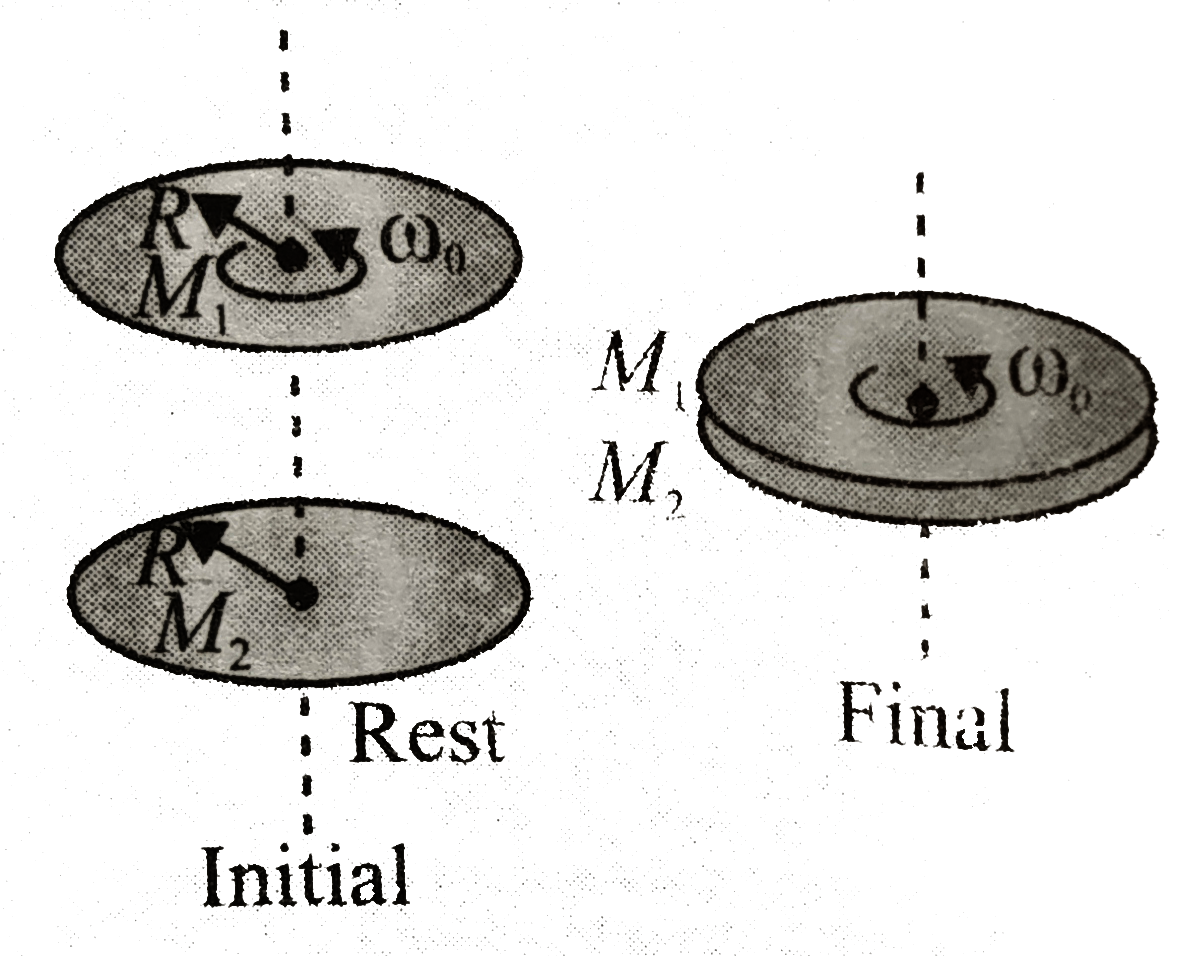Text Solution
Verified by Experts
Topper's Solved these Questions
RIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Exercise 3.3|21 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Exercise 3.4|13 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Exercise 3.1|11 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Integer|11 VideosSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS|Exercise Integer|16 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 2-Exercise 3.2
- A circular disc of mass M(1) and radius R, initially moving, With a co...
Text Solution
|
- A child of mass m is standing, on the periphery of a circular platform...
Text Solution
|
- Suppose in the previous poroblem, the child stays at rest on the platf...
Text Solution
|
- Consider a cylinder rolling on a horizontal plane. Its linear velocity...
Text Solution
|
- A particle of mass m is released from rest at point A in Fig., falling...
Text Solution
|
- Discs A and B are mounted on a shaft SS and may be connected or discon...
Text Solution
|
- A cicular disc of mass m and radius R is set into motion on a horizont...
Text Solution
|
- A particle of mass m is projected with a speed u at an angle theta to ...
Text Solution
|
- Point masses m(1) and m(2) are placed at the opposite ends of a rigid ...
Text Solution
|
- A thin uniform circular disc of mass M and radius R is rotating in a h...
Text Solution
|
- A thread is passing through a hole at the centre of frictionless table...
Text Solution
|
- A girl jumps from a height h on the end of a see-saw. The see-saw cons...
Text Solution
|
- The device shown in Fig. rotates on the vertical axle as shown. The fr...
Text Solution
|