Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
FLUID MECHANICS
CENGAGE PHYSICS|Exercise Single Correct|95 VideosFLUID MECHANICS
CENGAGE PHYSICS|Exercise Multipe Correct|15 VideosFLUID MECHANICS
CENGAGE PHYSICS|Exercise Exercise 4.4|10 VideosDIMENSIONS & MEASUREMENT
CENGAGE PHYSICS|Exercise Integer|2 VideosGRAVITATION
CENGAGE PHYSICS|Exercise INTEGER_TYPE|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-FLUID MECHANICS-Subjective
- Two immiscible liquids of densities rho and 2rho and thickness (height...
Text Solution
|
- A composite plate comprises a triangular area (1) and rectangular area...
Text Solution
|
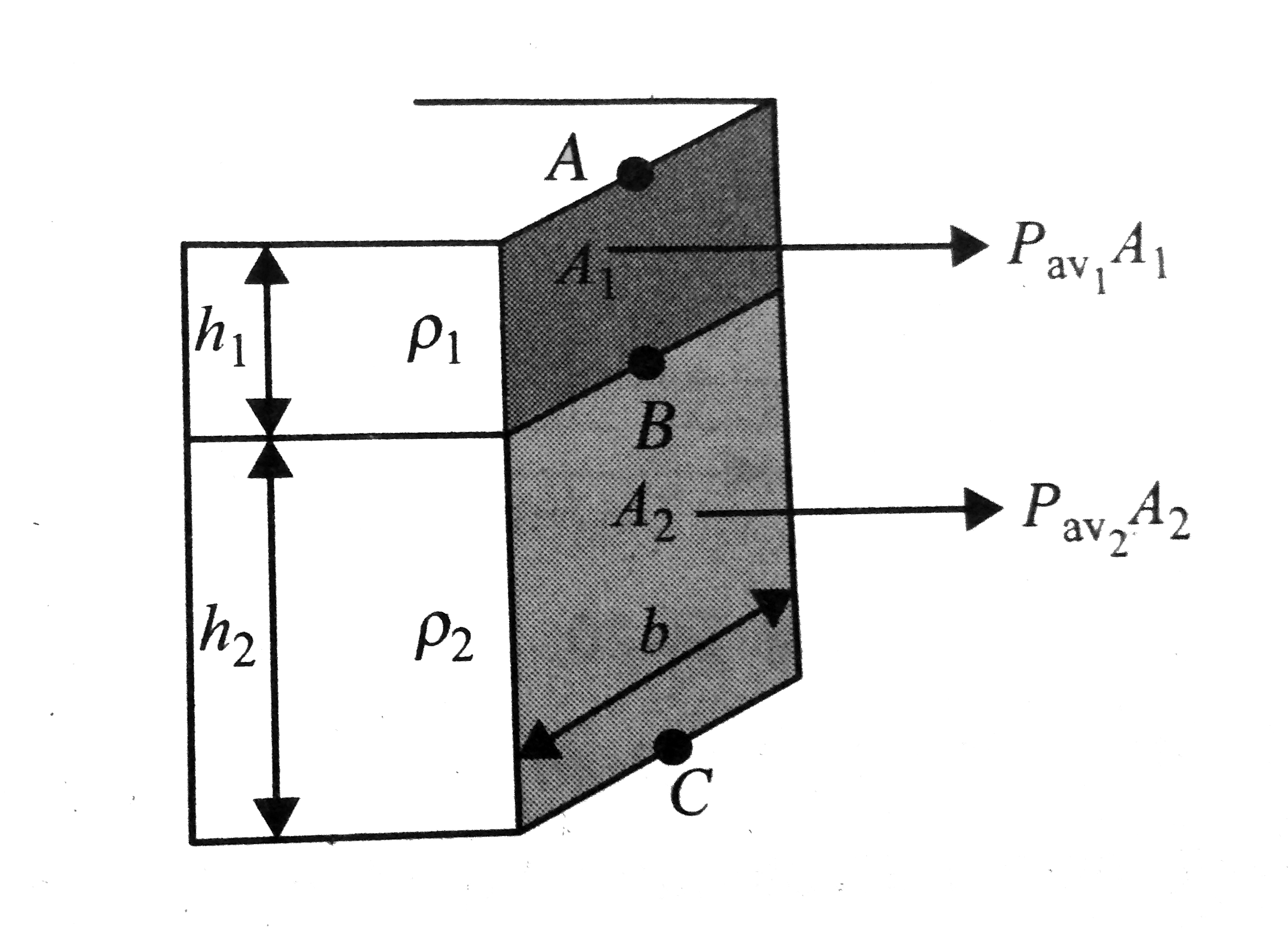
- A rectangular tube of uniform cross section has three liquids of densi...
Text Solution
|
- A simple accelerometer (an instrument for measuring acceleration) can ...
Text Solution
|
- A spherical tank of 1.2 m radius is half filled with oil of relative d...
Text Solution
|
- An expansible balloon filled with air is floating on the top surface o...
Text Solution
|
- An ice cube of side 1 cm is floating at the interface of kerosene and ...
Text Solution
|
- A cube of iron of edge 5 cm floats on the surface of mercury, containe...
Text Solution
|
- A wooden plank of length 1m and uniform cross-section is hinged at one...
Text Solution
|
- Oil enters the bend of a pipe in the horizontal plane with velocity 4m...
Text Solution
|
- Water is filled to a height of 2.5 m in a container lying rest on a ho...
Text Solution
|
- A tank with a small orifice contains oil on top of water. It is immers...
Text Solution
|
- A ball of weight W is supported on a vertical jet of water. If the str...
Text Solution
|
- A rocket ejects the fuel (hot gases) of density rho from the chamber w...
Text Solution
|
- A vertical U-tube has two liquids 1 and 2. The heights of liquids colu...
Text Solution
|
- A cup ABC is kept in a liquid of density rho as shown in the figure. F...
Text Solution
|
- A vertical U-tube is spinned about the vertical axis passing through t...
Text Solution
|
- A vertical U-tube has a liquid up to a height h. If the tube is slowly...
Text Solution
|
- A sphere is just immersed in a liquid. Find the ratio of hydrostatic f...
Text Solution
|
- The light cone is in equilibrium under the action of hydrostatic force...
Text Solution
|