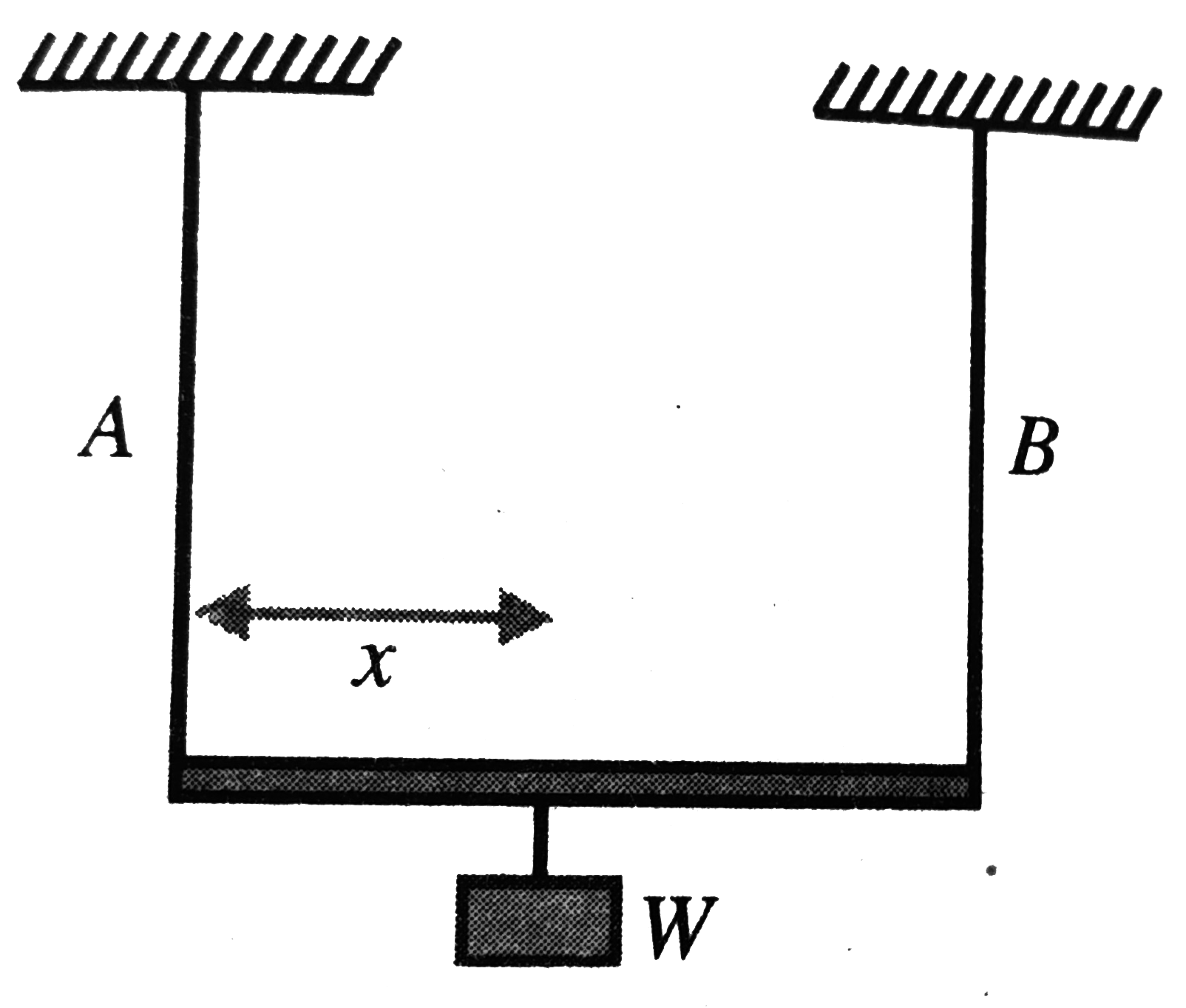
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise Integer|6 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise Fill In The Blanks|1 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise Assertion- Reasoning|13 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Integer type|1 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Integer|11 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-PROPERTIES OF SOLIDS AND FLUIDS-Linked Comprehension
- A light rod of length L=2 m is suspended horizontally from the ceiling...
Text Solution
|
- A light rod of length L=2 m is suspended horizontally from the ceiling...
Text Solution
|
- A lead sphere of 1.0 mm diameter and relative density 11.20 attains a ...
Text Solution
|
- A lead sphere of 1.0 mm diameter and relative density 11.20 attains a ...
Text Solution
|
- A long capillary tube of radius 0.2 mm is placed vertically inside a b...
Text Solution
|
- A long capillary tube of radius 0.2 mm is placed vertically inside a b...
Text Solution
|
- An oil of relative density 0.9 and viscosity 0.12 kg//ms flows through...
Text Solution
|
- An oil of relative density 0.9 and viscosity 0.12 kg//ms flows through...
Text Solution
|
- An oil of relative density 0.9 and viscosity 0.12 kg//ms flows through...
Text Solution
|
- A steel bolt of cross-sectional area A(b) = 5 xx 10^(-5) m^(2) is pass...
Text Solution
|
- A steel bolt of cross-sectional area A(b) = 5 xx 10^(-5) m^(2) is pass...
Text Solution
|
- A steel bolt of cross-sectional area A(b) = 5 xx 10^(-5) m^(2) is pass...
Text Solution
|
- On gradual loading , stress - strain relationship for a metal wire is ...
Text Solution
|
- On gradual loading , stress - strain relationship for a metal wire is ...
Text Solution
|
- According to Hooke's law, within the elastic limit stress/strain = con...
Text Solution
|
- Molecular forces exist between the molecules of a liquid in a containe...
Text Solution
|
- Molecular forces exist between the molecules of a liquid in a containe...
Text Solution
|
- Molecular forces exist between the molecules of a liquid in a containe...
Text Solution
|
- Materials get deformed when force is applied. Some of them regain thei...
Text Solution
|
- Materials get deformed when force is applied. Some of them regain thei...
Text Solution
|