A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
OSCILLATION AND SIMPLE HARMONIC MOTION
A2Z|Exercise Simple Pendulum And Different Cases Of Shm|25 VideosView PlaylistOSCILLATION AND SIMPLE HARMONIC MOTION
A2Z|Exercise Superposition Of Shm And Compound Pendulum|19 VideosView PlaylistOSCILLATION AND SIMPLE HARMONIC MOTION
A2Z|Exercise Velocity , Acceleration And Energy Of Simple Harmonic Motion|40 VideosView PlaylistNEWTONS LAWS OF MOTION
A2Z|Exercise Chapter Test|30 VideosView PlaylistPROPERTIES OF MATTER
A2Z|Exercise Chapter Test|29 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
A2Z-OSCILLATION AND SIMPLE HARMONIC MOTION-Spring Particle System
- Time period of a block when suspended from the upper plate of a parall...
01:37
|
Play - Two identical particle each of mass m are inter connects by a light sp...
01:40
|
Play - In figure S(1) andS(1) are identical springs. The oscillation frequenc...
02:24
|
Play - One end of a spring of force constant k is fixed to a vertical wall an...
03:18
|
Play - Three masses 700g and 500g and 400g are suspended at the end of a spri...
01:26
|
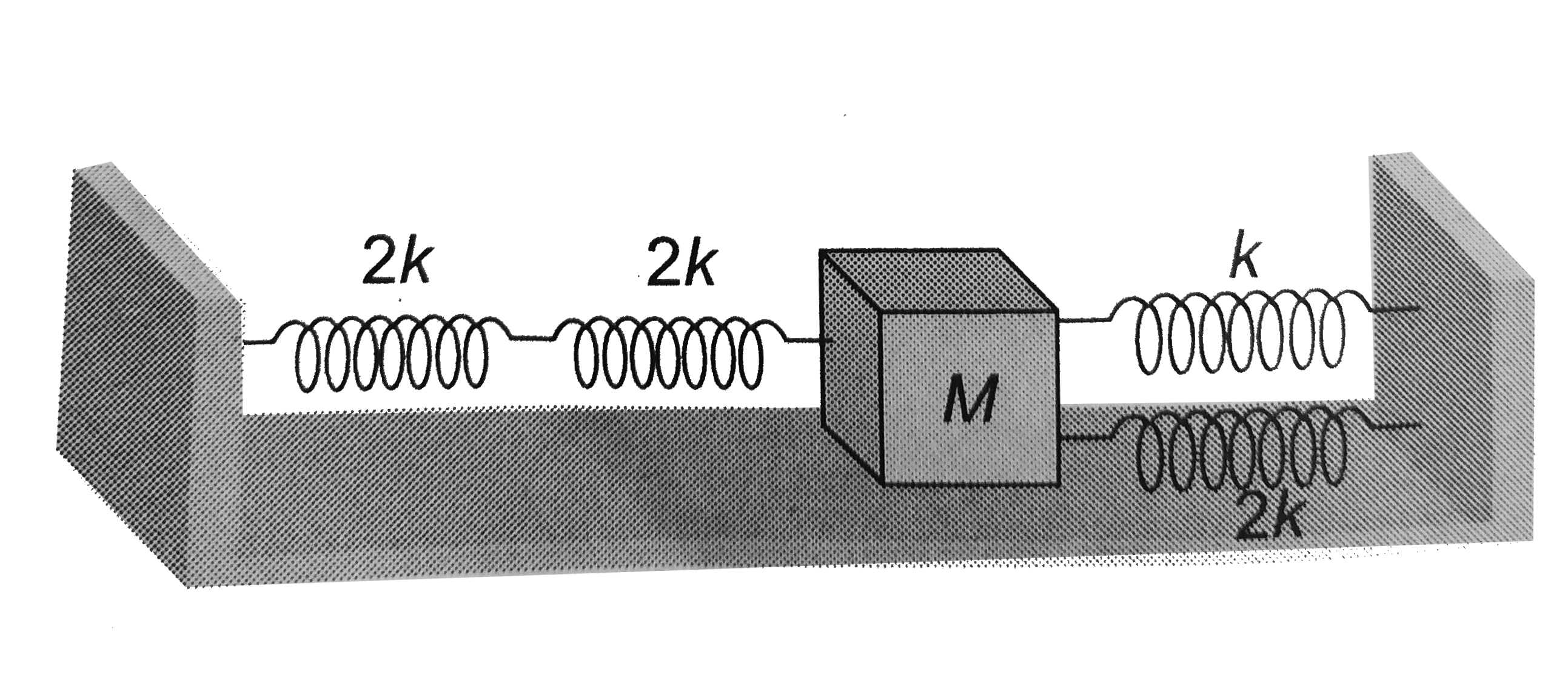
Play - Four massless spring whose force constant are 2k , 2k, k and 2k respec...
02:36
|
Playing Now - A particle at the end of a spring executes S.H,M with a period t(1)whi...
03:08
|
Play - Two identical spring are attached to a small block P The other ends of...
06:21
|
Play - Figure shows a system consisting of a massless pulley, a spring of for...
09:07
|
Play - A block of mass m is at rest on an another block of same mass as shown...
02:39
|
Play - Two particles (A) and (B) of equal masses are suspended from two massl...
02:21
|
Play - In the figure all spring are identical having spring constant k and ma...
01:15
|
Play - In the figure shown a block of masss m is atteched at ends of two spri...
01:09
|
Play - A force of 6.4N stretched a vertical spring by 0.1m .The mass that mus...
01:24
|
Play - A system is shown in the figure. The force The time period for small ...
01:52
|
Play - A block of mass m length force a verical of spring constant k If the b...
03:08
|
Play - A mass (M) is suspended from a spring of negligible mass. The spring i...
01:52
|
Play - A spring of spring constant K is cut equal parts of which t part are p...
03:16
|
Play - In a horizontal spring - mass m is released after being displaced tow...
02:35
|
Play - In the previous question, the amplitude of the oscillation is
02:20
|
Play