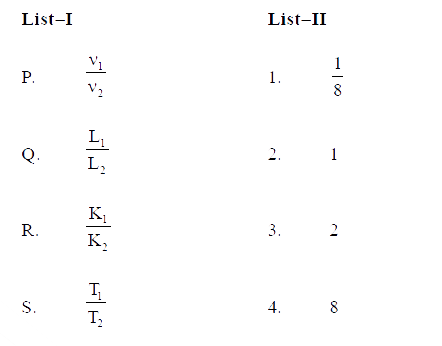A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
MODERN PUBLICATION|Exercise COMPETITION FILE (Matrix Match Type Questions)|3 VideosGRAVITATION
MODERN PUBLICATION|Exercise COMPETITION FILE (Integer Types questions)|12 VideosGRAVITATION
MODERN PUBLICATION|Exercise COMPETITION FILE ( Assertion Reasion Type Questions)|12 VideosMATHEMATICAL TOOLS
MODERN PUBLICATION|Exercise PRACTICE PROBLEMS (10)|12 Videos
Similar Questions
Explore conceptually related problems