Text Solution
Verified by Experts
Topper's Solved these Questions
AREAS OF TRIANGLES AND QUADRILATERALS
RS AGGARWAL|Exercise Exercise 14|32 VideosAREAS OF TRIANGLES AND QUADRILATERALS
RS AGGARWAL|Exercise EXERCISE|12 VideosAREAS OF TRIANGLES AND QUADRILATERALS
RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|16 VideosAREAS OF PARALLELOGRAMS AND TRIANGLES
RS AGGARWAL|Exercise ASSERTION & REASON TYPE|5 VideosBAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
RS AGGARWAL|Exercise EXERCISE 17B|16 Videos
Similar Questions
Explore conceptually related problems
RS AGGARWAL-AREAS OF TRIANGLES AND QUADRILATERALS-EXAMPLE
- The adjacent sides of a parallelogram ABCD are AB = 34 cm, BC = 20 cm ...
Text Solution
|
- Find the area of the parallelogram ABCD in which BC = 12 cm, CD = 17 c...
Text Solution
|
- In the given figure, ABCD is a rectangle of length 51 cm and bredth 25...
Text Solution
|
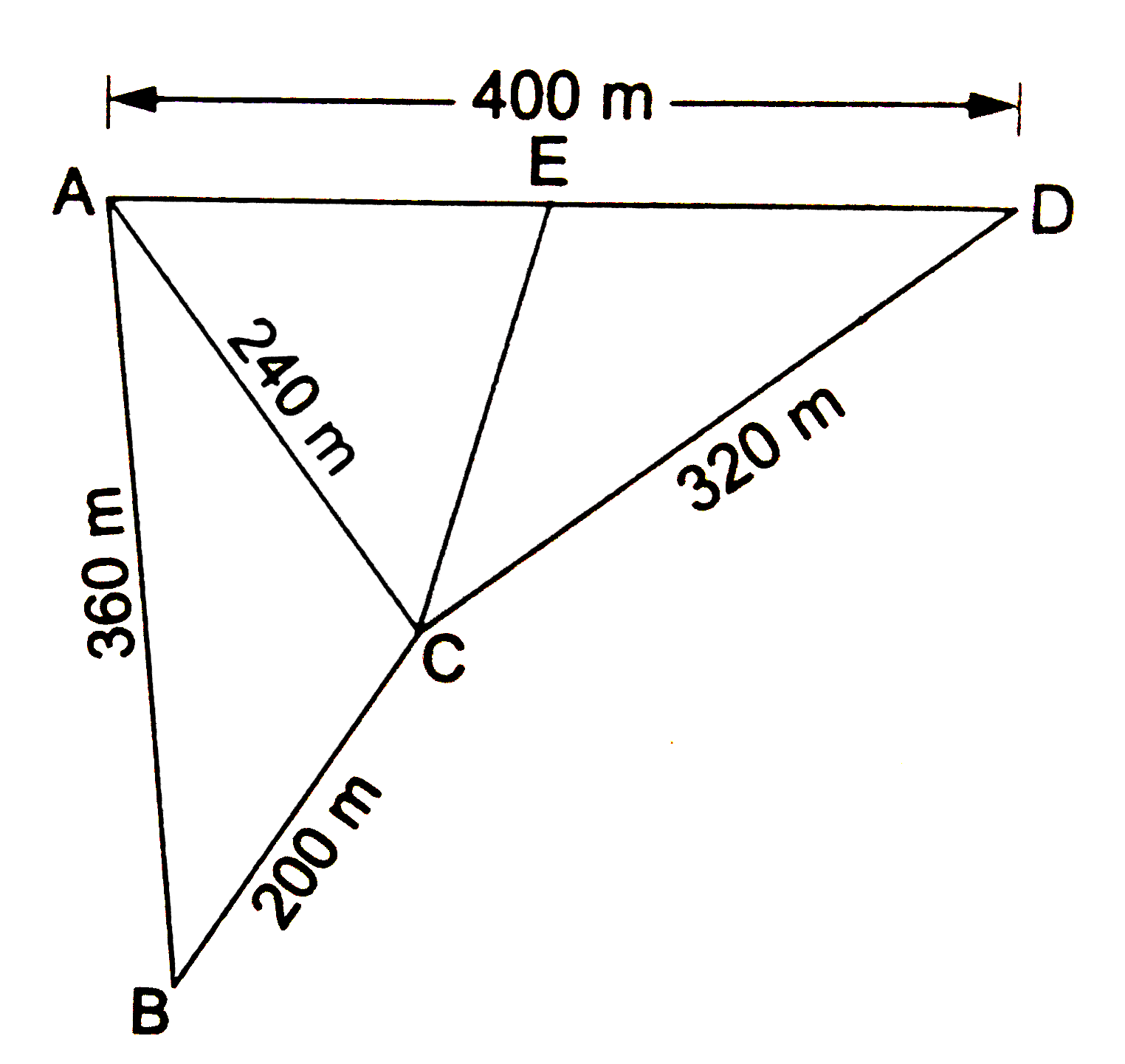
- A farmer has a triangular field with sides 360 m, 200 m and 240 m, whe...
Text Solution
|
- Radha made a picture of an aeroplane with coloured paper as shown in f...
Text Solution
|
- A kite in the shape of a square with a diagonal 32 cm and an isosceles...
Text Solution
|